 |
En cirkel er let at lave: Tegn en kurve, der er “radius” væk fra et centralt punkt. Og så: Alle punkter er i samme afstand fra centrum. |

Du kan tegne det selv
Sæt en nål i et tavle, læg en løkke med snor omkring den og indsæt en blyant i løkken. Hold strengen strakt og træk cirklen!
Spil med det
Prøv at trække punktet for at se, hvordan radius og omkreds ændrer sig.
(Se om du kan beholde en konstant radius!)
Radius, diameter og omkreds

Radius er afstanden fra centrum udad.
Diameteren går lige over cirklen gennem midten.
Omkredsen er afstanden en gang rundt om cirklen.
Og her er den virkelig seje ting:
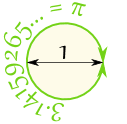
Når vi deler omkredsen med diameteren, får vi 3.141592654 …
som er nummer π (Pi)
|
Så når diameteren er 1, er omkredsen 3.141592654 … |
 |
Vi kan sige:
Omkreds = π × Diameter
Eksempel: Du går omkring en cirkel, der har en diameter på 100m, hvor langt er du gået?
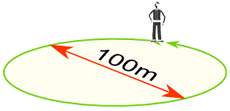
Afstand gået = Omkreds = π × 100m
= 314m (til nærmeste m)
Bemærk også, at Diameteren er dobbelt så stor som Radius:
Diameter = 2 × Radius
Og det gælder også:
Omkreds = 2 × π × Radius
Sammenfattende:
| × 2 | × π |
| |
|
| Radius | Diameter | Omkreds |
Huskning
Ordlængden kan hjælpe dig med at huske:
- Radius er det korteste ord og kort est mål
- Diameter er længere
- Omkreds er den længste
Definition
 |
Cirklen er en plan form (todimensionel), så: |
Cirkel: sæt af alle punkter i et plan, der er en fast afstand fra et centrum.
Område

Området for en cirkel er π gange radius i kvadrat, hvilket er skrevet:
A = π r2
Hvor
- A er området
- r er radius
For at hjælpe dig med at huske at tænke “Pie Are Squared” (selvom tærter normalt er runde):

Eksempel: Hvad er arealet af en cirkel med en radius på 1,2 m?
Eller ved hjælp af Diameter:

A = (π / 4) × D2
Areal sammenlignet med en firkant

En cirkel har ca. 80% af arealet af en kvadrat med samme bredde.
Den aktuelle værdi er (π / 4) = 0.785398 .. . = 78,5398 …%
Og noget interessant for dig:
Se Circle Area by Lines
Navne
Fordi folk har studerede cirkler i tusinder af år er der kommet specielle navne.
Ingen vil sige “den linje, der starter ved den ene side af cirklen, går gennem midten og slutter på den anden side” når de bare kan sig “Diameter”.
Så her er de mest almindelige specielle navne:
Linjer

En linje, der” lige rører “cirklen, når den passerer forbi, kaldes en tangent.
En linje, der skærer cirklen ved to punkter kaldes en sekant.
Et linjesegment, der går fra et punkt til et andet på cirkelens omkreds kaldes et akkord.
Hvis det passerer gennem midten kaldes det en diameter.
Og en del af omkredsen kaldes en bue.

Skiver
Der er to “skiver” i en cirkel.
“Pizza” -skiven kaldes en sektor.
Og skiven lavet af en akkord kaldes et segment.
Fælles sektorer
Kvadranten og halvcirklen er to specielle typer sektorer:

Kvart af en cirkel kaldes et kvadrant.

En halv cirkel kaldes en halvcirkel.
Inde og ude

En cirkel har en indvendig og en udvendig (selvfølgelig!). Men det har også et “til”, fordi vi kunne være lige på cirklen.
Eksempel: “A” er uden for cirklen, “B” er inde i cirklen og “C” er på cirklen .

Ellipse
En cirkel er et “specielt tilfælde” af en ellips.