(pi = 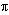= 3.141592 …)

Volymformler

Var försiktig !! Enheter räknas. Använd samma enheter för alla mätningar. Exempel

kub = a 3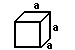

rektangulärt prisma = abc

oregelbundet prisma = bh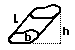

cylinder = bh = pi r 2 h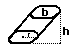

pyramid = (1/3) bh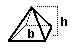

kon = (1/3) bh = 1/3 pi r 2 h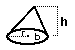

sfär = (4/3) pi r 3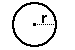

ellipsoid = (4 / 3) pi r1 r2 r3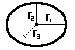

Enheter

Volymen mäts i ”kubiska” enheter. Volymen på en figur är antalet kuber som krävs för att fylla den helt, som block i en låda.

Kubens volym = sido gånger sido gånger sida. Eftersom varje sida av en fyrkant är densamma kan den helt enkelt vara längden på ena sidan.

Om en kvadrat har en sida på 4 tum, skulle volymen vara 4 tum gånger 4 tum gånger 4 tum eller 64 kubikcentimeter. (Kubikcentimeter kan också skrivas in3.)

Var noga med att använda samma enheter för alla mätningar. Du kan inte multiplicera fot gånger tum gånger meter, det gör inte ett perfekt kubiskt mått.

Volymen på ett rektangulärt prisma är längden på sidan gånger bredden gånger höjden. Om bredden är 4 tum, längden är 1 fot och höjden är 3 fot, vad är volymen?

INTE KORREKT …. 4 gånger 1 gånger 3 = 12

KORREKT … . 4 tum är samma som 1/3 fot. Volymen är 1/3 fot gånger 1 fot gånger 3 fot = 1 kubikfot (eller 1 cu. Ft. Eller 1 ft3).