Thevenins teorem säger att det är möjligt att förenkla vilken linjär krets, oavsett hur komplex, till en ekvivalent krets med bara en enda spänningskälla och seriemotstånd anslutet till en belastning. Kvalificeringen av ”linjär” är identisk med den som finns i Superposition Theorem, där alla underliggande ekvationer måste vara linjära (inga exponenter eller rötter). Om vi har att göra med passiva komponenter (såsom motstånd och senare, induktorer och kondensatorer Det är sant. Det finns dock vissa komponenter (särskilt vissa gasurladdnings- och halvledarkomponenter) som är olinjära: det vill säga deras motstånd mot strömförändringar med spänning och / eller ström. Som sådan skulle vi kalla kretsar som innehåller dessa typer av komponenter, icke-linjära kretsar.
Thevenins teorem i kraftsystem
Thevenins teorem är särskilt användbart vid analys av kraftsystem och andra kretsar där ett särskilt motstånd i kretsen (kallas ”belastning ”Motstånd) kan komma att ändras och omberäkning av kretsen är nödvändig för varje testvärde för belastningsmotstånd för att bestämma spänningen över den och strömmen genom den. Låt oss titta igen på vårt exempel på kretsar:

Låt oss anta att vi bestämmer oss för att beteckna R2 som ”belastnings” -motstånd i Vi har redan fyra analysmetoder (grenström, nätström, Millmans teorem och superpositionssats) att använda för att bestämma spänningen över R2 och ström genom R2, men var och en av dessa metoder är tidskrävande. Tänk dig att upprepa någon av dessa metoder om och om igen för att hitta vad som skulle hända om lastmotståndet ändrades (förändring av belastningsmotstånd är mycket vanligt i kraftsystem, eftersom flera belastningar slås på och av efter behov. Det totala motståndet för deras parallella anslutningar ändras beroende på hur många som är anslutna åt gången). Detta kan potentiellt innebära mycket arbete!
Thevenin Equivalent Circuit
Thevenins teorem gör det enkelt genom att tillfälligt ta bort lastmotståndet från original krets och reducera vad som är kvar till en motsvarande cir Cuit består av en enda spänningskälla och seriemotstånd. Lastmotståndet kan sedan återanslutas till denna ”Thevenin-ekvivalenta krets” och beräkningar utförs som om hela nätverket bara var en enkel seriekrets:

.. efter Thevenin-omvandlingen..
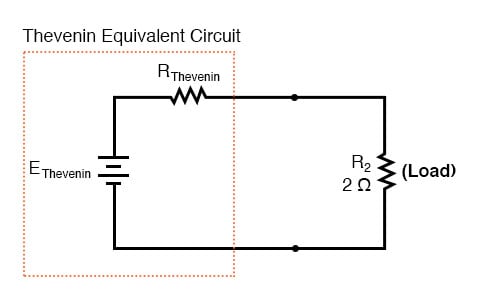
”Thevenin Equivalent Circuit” är den elektriska ekvivalenten för B1, R1, R3 och B2 sett från de två punkter där vårt belastningsmotstånd (R2) ansluter.
Thevenin-ekvivalenta kretsen, om den härleds korrekt, kommer att uppträda exakt samma som den ursprungliga kretsen bildad av B1, R1, R3 och B2. Med andra ord bör belastningsmotståndsspänningen (R2) och strömmen vara exakt samma för samma värde för belastningsmotståndet i de två kretsarna. Lastmotståndet R2 kan inte ”säga skillnaden” mellan det ursprungliga nätverket av B1, R1, R3 och B2, och Thevenin-ekvivalenta kretsen för EThevenin och RThevenin, förutsatt att värdena för EThevenin och RThevenin har beräknats korrekt.
Fördelen med att utföra ”Thevenin-omvandlingen” till den enklare kretsen är naturligtvis att det gör belastningsspänning och lastström så mycket lättare att lösa än i det ursprungliga nätverket. Att beräkna motsvarande Thevenin-källspänning och seriemotstånd är faktiskt ganska enkelt. Först avlägsnas det valda belastningsmotståndet från den ursprungliga kretsen, ersätts med ett brott (öppen krets):

Bestäm Thevenin Spänning
Därefter bestäms spänningen mellan de två punkter där lastmotståndet brukade anslutas. Använd de analysmetoder som finns till ditt förfogande för att göra detta. I det här fallet är den ursprungliga kretsen med lastmotståndet borttaget inget annat än en enkel seriekrets med motstående batterier, och så kan vi bestämma spänningen över de öppna belastningsterminalerna genom att tillämpa reglerna för seriekretsar, Ohms lag och Kirchhoffs spänning Lag:

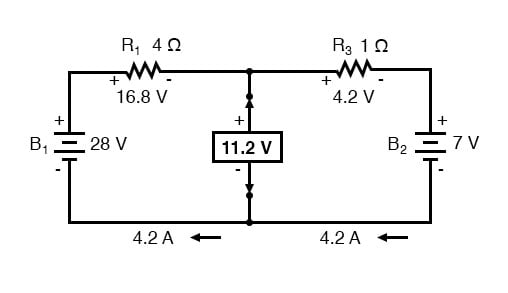
Spänningen mellan de två belastningsanslutningspunkterna kan räknas ut från en av batteriets spänningar och en av motståndets spänningar sjunker och blir 11,2 volt.Detta är vår ”Theveninspänning” (EThevenin) i ekvivalent krets:

Bestäm Thevenin Series Resistance
För att hitta Thevenin-seriens motstånd för vår ekvivalenta krets, måste vi ta den ursprungliga kretsen (med lastmotståndet fortfarande borttaget), ta bort strömkällorna (i samma stil som vi gjorde med Superposition Theorem: spänningskällor ersatta med ledningar och strömkällor ersatta med brott) och räknar motståndet från en belastningsterminal till den andra:

Med borttagningen av de två batterierna är det totala motståndet uppmätt vid denna plats lika med R1 och R3 parallellt: 0,8 Ω. Detta är vårt ”Thevenin-motstånd” (RThevenin) för motsvarande krets:

Bestäm spänningen över belastningsmotståndet
Med lastmotståndet (2 Ω) anslutet mellan anslutningspunkterna kan vi bestämma spänningen över den och ström genom det som om hela nätverket bara var en enkel seriekrets:

Observera att spännings- och strömvärdena för R2 (8 volt, 4 ampere) är identiska med de som hittades med andra analysmetoder. Observera också att spännings- och strömvärdena för Thevenin-seriens motstånd och Thevenin-källan (totalt) inte gäller någon komponent i den ursprungliga, komplexa kretsen. Thevenins teorem är bara användbart för att bestämma vad som händer med ett enda motstånd i ett nätverk: belastningen.
Fördelen är naturligtvis att du snabbt kan bestämma vad som skulle hända med det enda motståndet om det vore av ett annat värde än 2 Ω utan att behöva gå igenom mycket analys igen. Anslut bara det andra värdet för lastmotståndet till Thevenin-ekvivalenta kretsen och lite seriekretsberäkning ger dig resultatet.
ÖVERSIKT:
- Thevenins teorem är ett sätt att reducera ett nätverk till en motsvarande krets som består av en enda spänningskälla, seriemotstånd och serielast.
- Steg att följa för Thevenins teorem:
- Hitta Thevenin-källspänningen genom att ta bort lastmotståndet från den ursprungliga kretsen och beräkna spänningen över de öppna anslutningspunkterna där lastmotståndet var.
- Hitta Thevenin-motståndet genom att ta bort alla strömkällor i den ursprungliga kretsen (spänningskällor kortslutna och strömkällor är öppna) och beräknar totalt motstånd mellan de öppna anslutningspunkterna.
- Rita Thevenin-ekvivalentkretsen, med Thevenins spänningskälla i serie med Thevenin-motståndet. Lastmotståndet återansluts mellan de två öppna punkterna i motsvarande krets.
- Analysera spänning och ström för belastningsmotståndet enligt reglerna för seriekretsar.
RELATERAT ARBETSBLAD:
- Thevenins, Nortons och Maximum Power Transfer Theorems Worksheet