A summan är resultatet av ett tillägg. Till exempel ger 1, 2, 3 och 4 summan 10, skriven
 |
(1)
|
Siffrorna som summeras kallas tillägg eller ibland sommar. Summationsoperationen kan också anges med hjälp av en versal med stora och nedre gränser skrivna ovan och under och indexet nedan. Till exempel kan ovanstående summa skrivas
 |
(2)
|
The summan av en lista med siffror implementeras som Totalt.
En summa
 |
(3)
|
där varje term 
ges av någon fast regel (dvs. 
är en brunn -definierad sekvens) kallas en (ändlig) serie, och om antalet termer 
är oändligt kallas summan en oändlig serie (eller ofta bara en ”serie”). En summa av formuläret
 |
(4)
|
kallas en geometrisk serie .
Villkor för konvergens av en serie kan bestämmas i Wolfram-språket med hjälp av SumConvergence.
Den allmänna begränsade effekt summan
 |
(5)
|
kan ges med uttrycket
 |
(6)
|
vilket motsvarar Faulhabers formel, där notationen 
betyder kvantiteten i frågan lyfts till lämplig kraft 
och alla villkor i formuläret 
ersätts med motsvarande Bernoulli siffror 
.
En underhållande identitet på grund av J. Ziegenbein (pers. komm. 19 juni 2002) följer av identiteten
 |
(7)
|
som kan skrivas
 |
(8)
|
Därför 
kan till exempel skrivas i motsvarande former
 |
 |
 |
(9)
|
 |
 |
 |
(10)
|
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
och så vidare.
Nicomachus sats ger som nyfiken uttryck för maktsumman 
.
Specialsummor inkluderar
 |
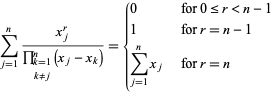(13)
|
och
 |
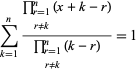(14)
|
För att minimera summan av en uppsättning rutor av siffror 
om ett givet nummer 
 |
 |
 |
(15 )
|
 |
 |
 |
(16)
|
ta derivatet.
 |
(17)
|
Lös för 
ger
 |
(18)
|
så 
minimeras när 
är inställt på menar.