Introduktion till k-närmaste grannar: En kraftfull maskininlärningsalgoritm (med implementering i Python & R)

Obs! Den här artikeln publicerades ursprungligen den 10 oktober 2014 och uppdaterades den 27 mars 2018

Översikt

• Förstå k närmaste granne (KNN) – en av de mest populära algoritmerna för maskininlärning
• Lär dig hur kNN fungerar i python
• Välj rätt värde på k i enkla termer

Introduktion

Under de fyra åren av min datavetenskapskarriär har jag byggt mer än 80% klassificeringsmodeller och bara 15-20% regressionsmodeller. Dessa förhållanden kan mer eller mindre generaliseras i hela branschen. Anledningen till denna fördom mot klassificeringsmodeller är att de flesta analytiska problem handlar om att fatta ett beslut.

Till exempel kommer en kund attrita eller inte, om vi riktar oss mot kund X för digitala kampanjer, oavsett om kunden har en hög potential eller inte, etc. Analyserna är mer insiktsfulla och direkt kopplade till en implementeringskarta.

I den här artikeln kommer vi att prata om en annan allmänt använd klassificeringsteknik för maskininlärning som kallas K-närmaste grannar (KNN). Vårt fokus kommer främst att ligga på hur algoritmen fungerar och hur påverkar ingångsparametern utdata / förutsägelse.

Obs! Människor som föredrar att lära sig genom videor kan lära sig samma genom vår kostnadsfria kurs – K- Närmaste grannar (KNN) algoritm i Python och R. Och om du är en nybörjare för datavetenskap och maskininlärning, kolla in vårt certifierade BlackBelt-program –

• Certifierad AI & ML Blackbelt + -program

Innehållsförteckning

• När använder vi KNN-algoritm?
• Hur fungerar KNN-algoritm fungerar?
• Hur väljer vi faktorn K?
• Bryter ner den – Pseudokod för KNN
• Implementering i Python från grunden
• Jämföra vår modell med scikit-lär

När använder vi KNN-algoritm?

KNN kan användas för båda prediktiva problem med klassificering och regression. Det används dock mer i klassificeringsproblem i branschen. För att utvärdera vilken teknik som helst tittar vi generellt på tre viktiga aspekter:

1. Lätt att tolka utdata

2. Beräkningstid

3. Predictive Power

Låt oss ta några exempel för att placera KNN i skalan:

KNN-algoritm mäter över alla parametrar av överväganden. Det används ofta för sin enkla tolkning och låga beräkningstid.

Hur fungerar KNN-algoritmen?

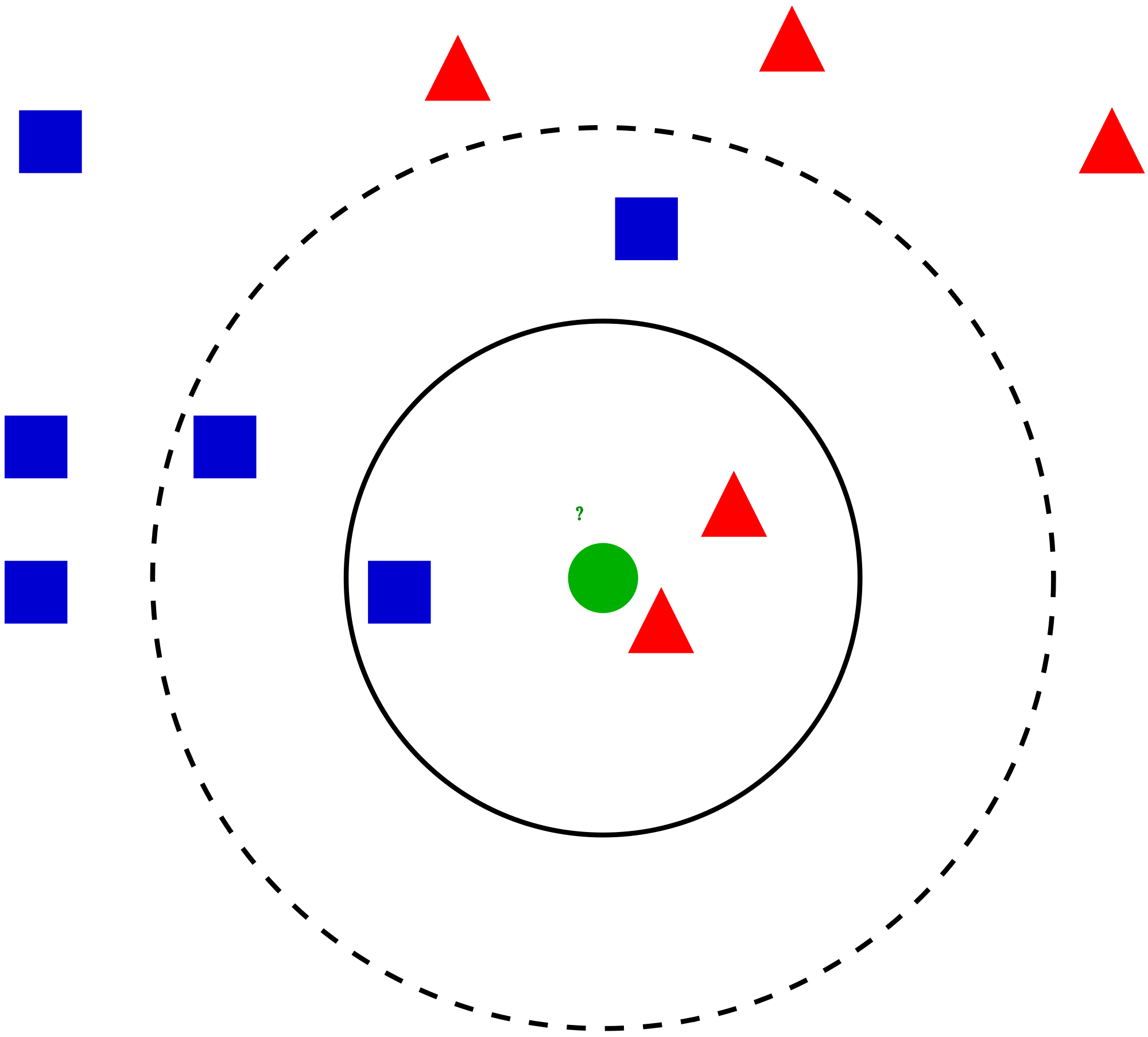
Låt oss ta ett enkelt fall till förstå denna algoritm. Följande är en spridning av röda cirklar (RC) och gröna rutor (GS):

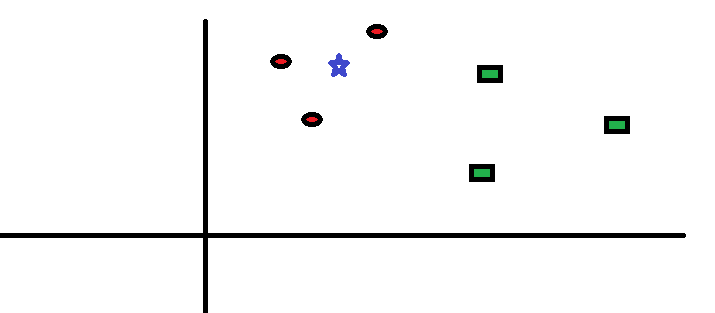Du tänker ta reda på klassen av den blå stjärnan (BS). BS kan antingen vara RC eller GS och ingenting annat. ”K” är KNN-algoritmen är den närmaste grannen vi vill ta omröstningen från. Låt oss säga K = 3. Därför kommer vi nu att göra en cirkel med BS som centrum lika stor som att endast bifoga tre datapunkter på planet Se följande diagram för mer information:

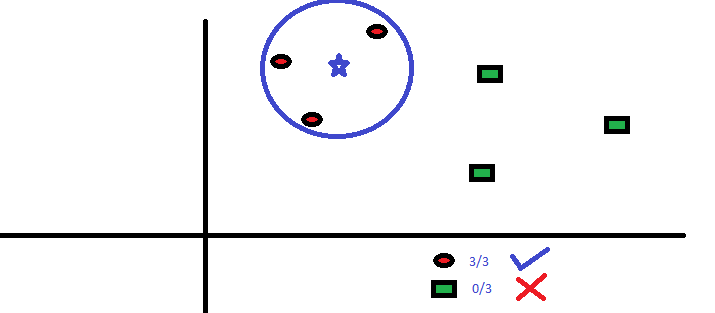De tre närmaste punkterna till BS är alla RC. med en bra konfidensnivå kan vi säga att BS borde tillhöra klassen RC. Här blev valet mycket uppenbart eftersom alla tre rösterna från närmaste granne gick till RC. Valet av parameter K är mycket avgörande i denna algoritm Därefter kommer vi att förstå vilka faktorer som ska anses vara de bästa K.

Hur väljer vi faktorn K?

Låt oss först försöka förstå vad exakt påverkar K i algoritmen. Om vi ser det sista exemplet, med tanke på att alla 6 träningsobservation förblir konstanta, med ett givet K-värde kan vi skapa gränser för varje klass. se gränser kommer att separera RC från GS. På samma sätt, låt oss försöka se effekten av värdet ”K” på klassgränserna. Följande är de olika gränserna som skiljer de två klasserna med olika värden på K.

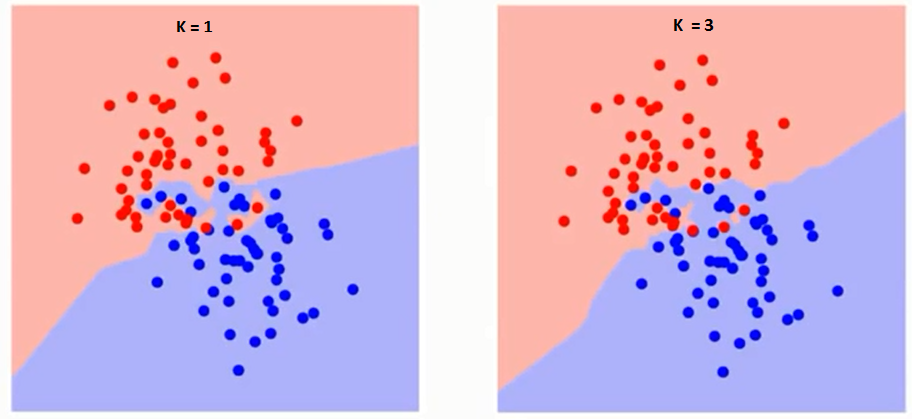
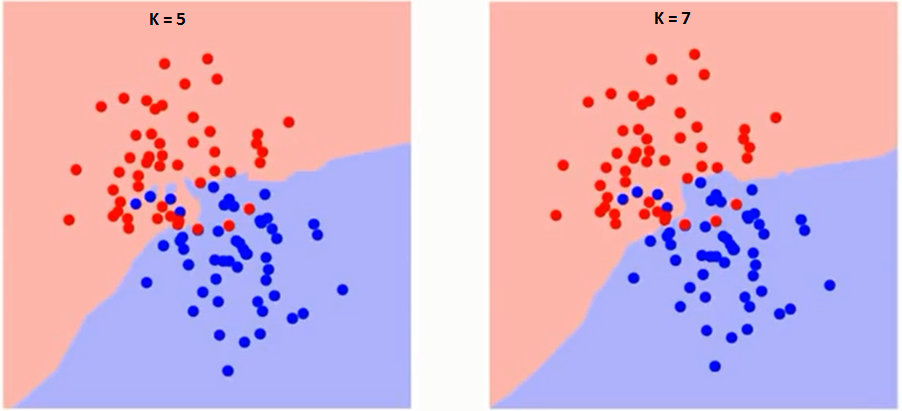
Om du tittar noga kan du se att gränsen blir mjukare med ökande värde av K. Med K som ökar till oändlighet blir det äntligen helt blått eller helt rött beroende på den totala majoriteten. Träningsfelfrekvensen och valideringsfelfrekvensen är två parametrar som vi behöver för att komma åt olika K-värde. Följande är kurvan för träningsfelfrekvensen med ett varierande värde på K:

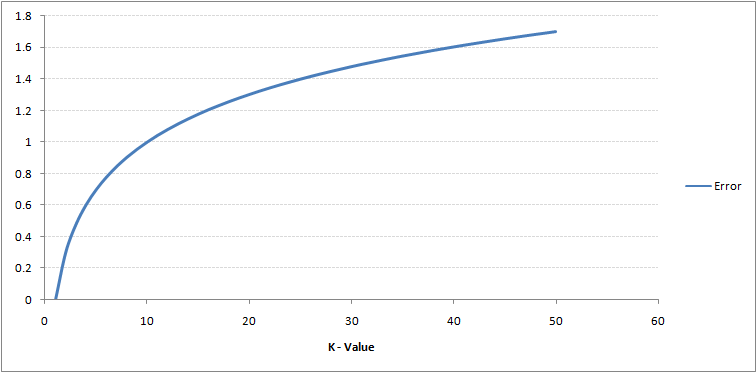Som du kan se, felfrekvensen vid K = 1 är alltid noll för träningsprovet.Detta beror på att den närmaste punkten till någon träningsdatapunkt är sig själv. Därför är förutsägelsen alltid korrekt med K = 1. Om valideringsfelkurvan skulle ha varit liknande skulle vårt val av K ha varit 1. Följande är valideringsfelkurvan med varierande värde på K:

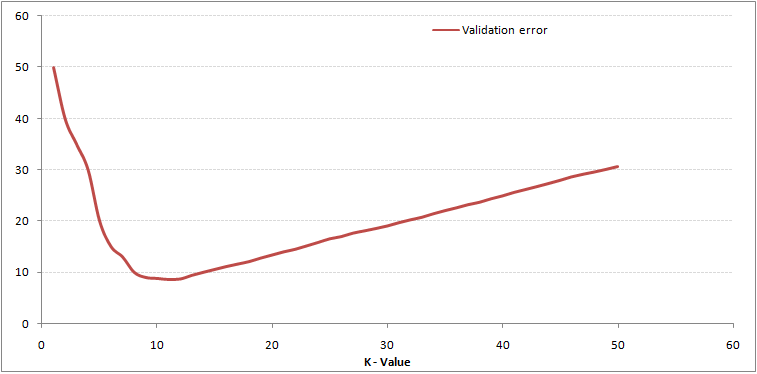Detta gör berättelsen tydligare. Vid K = 1 överanpassade vi gränserna. Följaktligen minskar felfrekvensen initialt och når ett minimum. Efter miniminivån ökar den med ökande K. För att få det optimala värdet av K kan du separera träning och validering från den ursprungliga datasetet. Rita nu upp valideringsfelkurvan för att få det optimala värdet av K. Detta värde av K ska användas för alla förutsägelser.

Ovanstående innehåll kan förstås mer intuitivt med vår kostnadsfria kurs – K-närmaste grannar ( KNN) Algoritm i Python och R

Bryta ner det – Pseudokod för KNN

Vi kan implementera en KNN-modell genom att följa nedanstående steg:

1. Ladda data
2. Initiera värdet på k
3. För att få den förutspådda klassen, iterera från 1 till totalt antal träningsdatapunkter
   1. Beräkna avståndet mellan testet data och varje rad träningsdata. Här kommer vi att använda euklidiskt avstånd som vårt avståndsmätvärde eftersom det är den mest populära metoden. De andra mätvärdena som kan användas är Chebyshev, cosinus, etc.
   2. Sortera de beräknade avstånden i stigande ordning baserat på avståndsvärden
   3. Få topp k-rader från den sorterade matrisen
   4. Få den vanligaste klassen av dessa rader
   5. Returnera den förutsagda klassen

Implementering i Python från grunden

Vi kommer att använda den populära Iris-datasetet för att bygga vår KNN-modell. Du kan ladda ner den härifrån.

Jämföra vår modell med scikit-lär

Vi kan se att båda modellerna förutspådde samma klass (Iris- virginica ) och samma närmaste grannar (). Därför kan vi dra slutsatsen att vår modell går som förväntat.

Implementering av kNN i R

Steg 1: Importera data

Steg 2: Kontrollera data och beräkning av datasammanfattningen

Output

Steg 3: Dela data

Steg 4: Beräkning det euklidiska avståndet

Steg 5: Skriva funktionen för att förutsäga kNN

Steg 6: Beräkna etiketten (Namn) för K = 1

Output

For K=1 "Iris-virginica"

På samma sätt kan du beräkna för andra värden för K.

Jämföra vår kNN-prediktorfunktion med ”Class” -biblioteket

Output

For K=1 "Iris-virginica"

Vi kan se att båda modeller förutspådde samma klass (Iris-virginica).

Slutanmärkningar

KNN-algoritm är en av de enklaste klassificeringsalgoritmerna. Även med sådan enkelhet kan det ge mycket konkurrenskraftiga resultat. KNN-algoritm kan också användas för regressionsproblem. Den enda skillnaden från den diskuterade metoden kommer att använda medelvärden för närmaste grannar snarare än att rösta från närmaste grannar. KNN kan kodas i en enda rad på R. Jag har ännu inte undersökt hur vi kan använda KNN-algoritmen i SAS.

Tyckte du att artikeln var användbar? Har du använt något annat maskininlärningsverktyg nyligen? Planerar du att använda KNN i något av dina affärsproblem? Om ja, dela med oss hur du planerar att göra det.

Om du gillar det du just läste & vill du fortsätta med din analytiska inlärning, prenumerera på vår e-post, följ oss på twitter eller gilla vår facebook-sida.