En klockkurva, även känd som normalfördelning, är den vanligaste distributionstypen för en variabel. Det accepteras som en distribution som förekommer naturligt i många situationer. I en klockkurva definierar den högsta punkten i bågen medelvärdet, vilket är det högsta antalet förekomster av ett element. Sannolikheten för händelser minskar mot vardera sidan av kurvan. Du kan använda en klockkurva för att jämföra prestanda genom att utesluta ytterligheter, eller definiera dina förväntningar genom möjligheten att ett resultat ligger inom ett område till vänster eller höger om mitten. I den här guiden kommer vi att visa dig hur du skapar en klockkurva i Excel med ett verklighetsscenario som exempel.
Ladda ner arbetsbok
Grunder
Allt du behöver är medelvärdet (genomsnittet) och standardavvikelsen för din datamängd. Båda dessa mätvärden kan beräknas i Excel med formlerna nedan.
Med hänsyn till dessa två värden följer normalt fördelade värden följande regler:
- Det totala området under kurvan är lika med 1 (100%)
- Klockkurvens centrum är medelvärdet för datapunkten
- (1-σ) Cirka 68,2% av arean under kurvan faller inom en standardavvikelse (medelvärde ± standardavvikelse)
- (2-σ) Cirka 95,5% av arean under kurvan faller inom två standardavvikelser (medelvärde ± 2 * standardavvikelse)
- (3-σ) Cirka 99,7% av arean under kurvan faller inom tre standardavvikelser (medelvärde ± 3 * standardavvikelse)
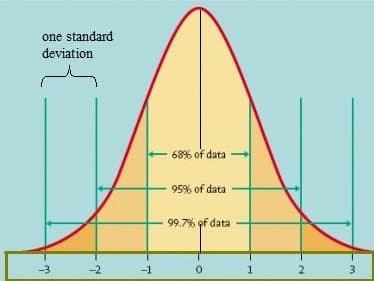
Bild från University of Virginia
Skapa en klockkurva i Excel
Låt oss ta ett vanligt exempel och säga att vi analyserar tentamen Det är för en klass elever. Vi använder en klockkurva för att mäta undersökningsresultat för bättre jämförelse.
Vi börjar med att beräkna mätvärdena för att generera en normalfördelad data som genererar vår kurva. Vi måste beräkna:
- Genomsnitt (medelvärde) av värdena.
- Standardavvikelsen för värdena.
- 3-standardavvikelsegränser för före och efter medelvärde.
- Intervallvärde för normalt distribuerade datapunkter. Detta kräver också en bestämning av intervallpunkterna. Du kan välja vilket nummer som helst, men kom ihåg att fler intervall betyder mer precision.
Mätvärden
Börja med att beräkna medelvärdet och standardavvikelsen för data. Du kan använda AVEREAGE- och STDEV.P-funktionerna för att beräkna medelvärden respektive standardavvikelser.

Nästa steg beräknas de tre standardavvikelsevärdena för att ställa in minimi- och maximivärdena för 99,7% av datan.

Maximum = 83,23 – 3 * 5,54 = 99,86
När vi har ställt in minsta och högsta värden för vår kurva, måste vi generera intervallen . Intervallvärdena är basen för de normalt distribuerade värdena. För att beräkna intervallen är allt du behöver göra att dela upp området mellan minimi- och maxvärdena efter intervallantal. I det här exemplet ställer vi in detta på 20, men du kan använda ett större antal för att öka antalet datapunkter.

När intervallvärdet har beräknats kan du generera datapunkterna. För att göra detta anger du minimivärdet i en cell. Rätt under minimivärdet anger du formeln för att lägga till intervallvärdet till minimumet. Här använde vi cellreferenser (som J4) som hjälper till att fylla datapunkterna upp till maximalt värde.

Nästa steg är att beräkna de normalt distribuerade värdena från de genererade datapunkterna. Du kan använda Excels funktion NORM.DIST för att generera dessa värden.
Använd de befolkade datapunkterna som det första argumentet för funktionen. Medel- och standardavvikelsevärdena är nästa argument. Avsluta formeln med ett FALSE booleskt värde för att använda icke-kumulativ typ av denna funktion.

Diagram
Vi är nästan klara! Välj datapunkter och normalfördelningsvärden och infoga sedan ett X-Y Scatter-diagram. Använd versionen Scattered with Smooth Lines för att skapa en kurva i Excel.

Diagrammet kan tyckas vara lite av först.Låt oss se hur du kan få det att se bättre ut.
För att ändra diagrammets titel, dubbelklicka på titeln och uppdatera namnet.
Därefter dubbelklickar du på X-axel och definiera minimi- och maxvärden från axelalternativpanelen för att eliminera det vita utrymmet på båda sidor. Detta ger ditt diagram en bättre klockform. Vi ställer in värden som ligger lite utanför vår datamängd. Till exempel 66 – 100 för värden 66.30 – 99.86.
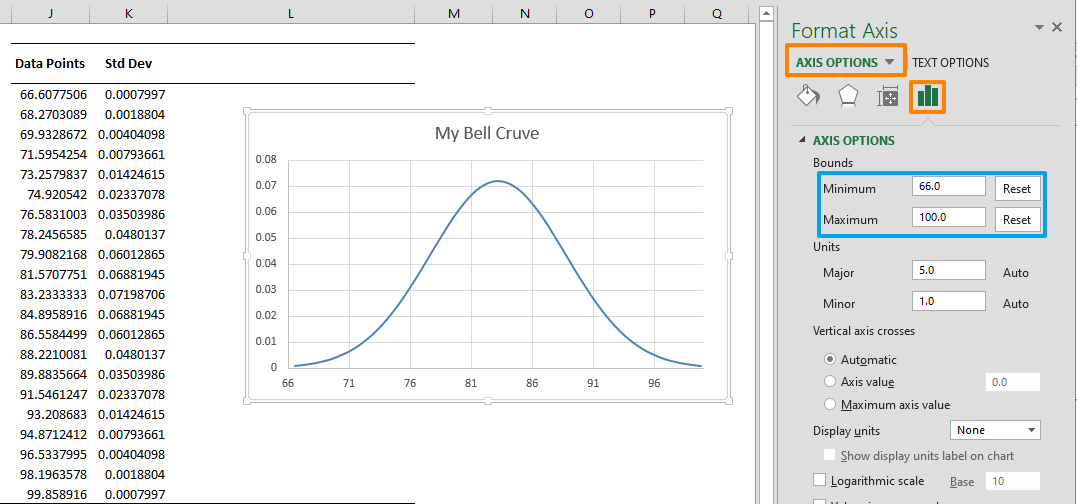
Du kan ytterligare förbättra ditt diagram genom att lägga till standardavvikelsevärdena .
