Lutning
Förutom dess välbekanta betydelse har ordet ”sluttning” exakt matematisk betydelse. Lutningen på en linje är stigningen under körningen, eller förändringen i y dividerat med förändringen i x. Välj två punkter på linjen för att hitta lutningen på en linje. Sedan subtraherar deras x-koordinater och subtraherar deras y-koordinater i samma ordning. Dela skillnaden mellan y-koordinaterna med skillnaden mellan x- koordinaterna:
Givet två punkter (x1, y1) och (x2, y2) på en rad är lutningens lutning lika med:
m = =
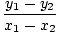
Negativ lutning
Om en linje har en positiv lutning (dvs. m > 0), då ökar alltid y när x ökar och y minskar alltid när x minskar. Således börjar linjens graf längst ned till vänster och går uppåt till höger.
Ofta är lutningen på en linje dock negativ. En negativ lutning innebär att y alltid minskar när x ökar och y alltid ökar när x minskar. Här är ett exempel på en graf med negativ lutning:
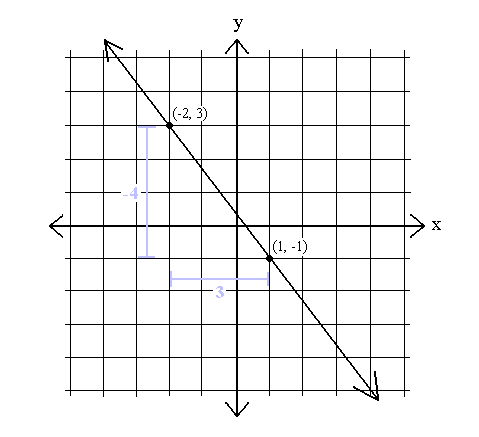
m =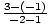 
= 
= – 
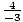Såsom x ökar med 3 minskar y med 4, och när x minskar med 3, ökar y med 4.
Horisontella och vertikala linjer
Ibland kommer vi att se ekvationer vars grafer är horisontella linjer. Dessa är grafer där y förblir konstant – det vill säga där y1 – y2 = 0 för två punkter på raden:
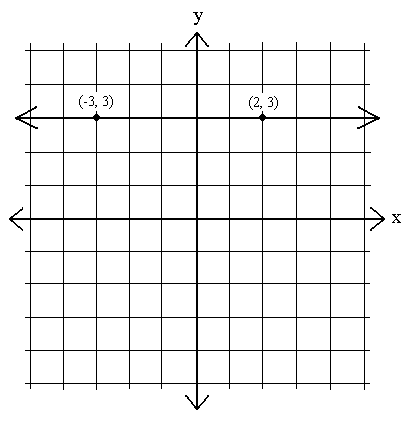
m =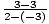 
= 
= 0.
Lutningen på vilken horisontell linje som helst är 0. Med andra ord, när x ökar eller minskar, ändras inte y. x tar alla möjliga värden till ett specifikt y-värde.
Vi kommer också att se ekvationer vars grafer är vertikala linjer. Dessa är grafer där x förblir konstant – det vill säga där x1 – x2 = 0 för alla två punkter på raden:
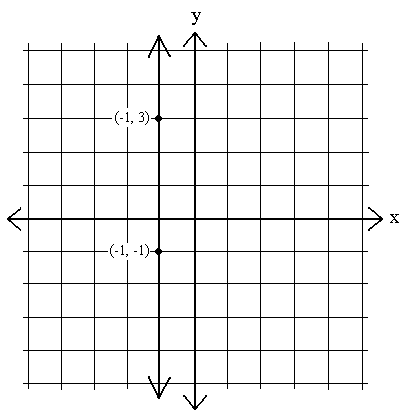
m =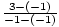 
= 
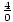= odefinierad. Vi kan inte dela ett tal med noll.
Lutningen på någon vertikal linje är odefinierad. X ökar eller minskar inte; snarare tar y alla möjliga värden vid ett specifikt x-värde.