Vad är BFS-algoritm (Breadth-First Search)?
Bredd-first search (BFS) är en algoritm som används för att rita data eller söka i träd eller genomkorsningsstrukturer. Den fullständiga formen av BFS är den bredaste sökningen.
Algoritmen besöker och markerar alla nyckelnoder effektivt i ett diagram på ett korrekt sätt på bredden. Denna algoritm väljer en enda nod (initial- eller källpunkt) i ett diagram och besöker sedan alla noder intill den valda noden. Kom ihåg att BFS får åtkomst till dessa noder en efter en.
När algoritmen besöker och markerar startnoden flyttas den mot närmaste obesökta noder och analyserar dem. Efter att ha besökt markeras alla noder. Dessa iterationer fortsätter tills alla noder i diagrammet har besökts och markerats.
I denna algoritmhandledning lär du dig:
- Vad är BFS-algoritm (Breadth-First Search)?
- Vad är grafgenomgångar?
- BFS-algoritmens arkitektur
- Varför behöver vi BFS-algoritm?
- Hur fungerar BFS-algoritm?
- Exempel på BFS-algoritm
- Regler för BFS-algoritm
- Tillämpningar på BFS-algoritm
Vad är diagramtrappor?
En grafgenomgång är en vanligt använd metod för att lokalisera toppunktpositionen i diagrammet. Det är en avancerad sökalgoritm som kan analysera grafen med hastighet och precision tillsammans med att markera sekvensen för de besökta hörnpunkterna. Denna process gör att du snabbt kan besöka varje nod i en graf utan att vara låst i en oändlig slinga.
Arkitekturen för BFS-algoritmen
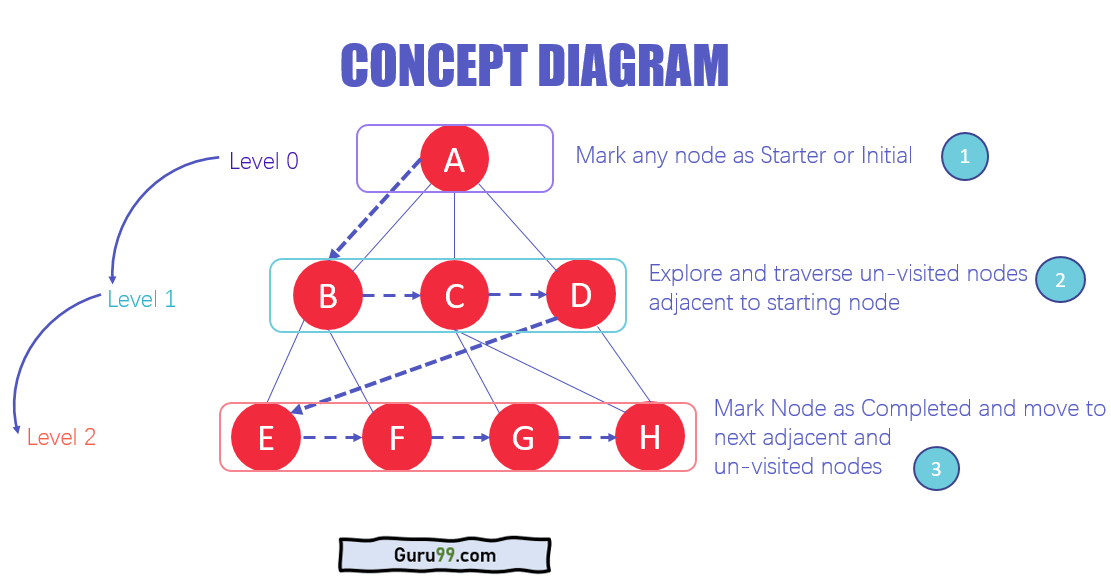
- I de olika nivåerna av data kan du markera vilken nod som helst eller initial nod för att börja korsa. BFS kommer att besöka noden och markera den som besökt och placera den i kön.
- Nu kommer BFS att besöka de närmaste och obesökta noder och markera dem. Dessa värden läggs också till i kön. Kön fungerar på FIFO-modellen.
- På liknande sätt analyseras de återstående närmaste och obesökta noderna i grafen markerade och läggs till i kön. Dessa objekt raderas från kön som mottagning och skrivs ut som resultat.
Varför behöver vi BFS-algoritm?
Det finns många anledningar att använda BFS-algoritmen för att söka efter din dataset. Några av de viktigaste aspekterna som gör denna algoritm till ditt första val är:
- BFS är användbart för att analysera noderna i en graf och konstruera den kortaste vägen att korsa genom dessa.
- BFS kan gå igenom ett diagram i det minsta antalet iterationer.
- BFS-algoritmens arkitektur är enkel och robust.
- Resultatet av BFS-algoritmen har hög noggrannhet jämfört med andra algoritmer.
- BFS-iterationer är sömlösa, och det finns ingen möjlighet att denna algoritm fastnar i ett oändligt loopproblem.
Hur fungerar BFS-algoritm?
Grafgenomgång kräver att algoritmen besöker, kontrollerar och / eller uppdaterar varje enskild obesökt nod i en trädliknande struktur. Grafgenomgångar kategoriseras efter den ordning de besöker noderna i diagrammet.
BFS-algoritm startar operationen från den första eller startnoden i ett diagram och går igenom den noggrant. När den väl korsat den ursprungliga noden besöks och markeras nästa icke-korsade toppunkt i diagrammet.
Därför kan du säga att alla noder intill det aktuella toppunktet besöks och passeras i den första iterationen. En enkel kömetodik används för att implementera arbetet med en BFS-algoritm, och den består av följande steg:
Steg 1)

Varje toppunkt eller nod i grafen är känd. Du kan till exempel markera noden som V.
Steg 2)

Om toppunkt V inte nås, lägg sedan till toppunkt V i BFS-kö
Steg 3)

Starta BFS-sökningen och markera toppunkt V som besökt efter avslutad.
Steg 4)

BFS-kön är fortfarande inte tomt, ta därför bort toppunktet V i diagrammet från kön.
Steg 5)

Hämta alla återstående hörn i diagrammet som ligger intill toppunktet V
Steg 6)

Låt oss säga V1 för varje intilliggande toppunkt, om det inte besöks ännu, lägg sedan till V1 i BFS-kön
Steg 7)

BFS kommer att besöka V1 och markera det som besökt och ta bort det från kön.
Exempel BFS-algoritm
Steg 1)

Du har en graf över sju siffror som sträcker sig från 0 – 6.
Steg 2)

0 eller noll har markerats som en rotnod.
Steg 3)

0 besöks, markeras och infogas i ködatastrukturen.
Steg 4)
Återstående 0 intilliggande och oviserade noder besöks, markeras och infogas i kön.
Steg 5)

Körande iterationer upprepas tills alla noder besöks.
Regler för BFS-algoritm
Här är viktiga regler för användning av BFS-algoritm:
- En kö (FIFO-först in först ut) datastruktur används av BFS.
- Du markerar vilken nod som helst i diagrammet som root och börjar korsa data från den.
- BFS korsar alla noder i diagrammet och släpper dem hela tiden som färdiga.
- BFS besöker en intilliggande obesökt nod, markerar den som klar och sätter in den i en kö.
- Tar bort föregående toppunkt från kön om inget intilliggande toppunkt hittas.
- BFS-algoritm upprepas tills alla hörn i diagrammet är framgångsrika och markerade som färdiga.
- Det finns inga slingor orsakade av BFS under korsningen av data från någon nod.
Tillämpningar av BFS-algoritm
Låt oss ta en titta på några av de verkliga applikationerna där en BFS-algoritmimplementering kan vara mycket effektiv.
- Oviktade grafer: BFS-algoritm kan enkelt skapa den kortaste vägen och ett minimalt spännande träd för att besöka alla kurvorna i diagrammet på kortast möjliga tid med hög noggrannhet.
- P2P-nätverk: BFS kan implementeras för att lokalisera alla närmaste eller närliggande noder i ett peer-to-peer-nätverk. Detta kommer att hitta nödvändiga data snabbare .
- Webbsökare: Sökmotorer eller webbsökare kan enkelt bygga flera nivåer av index genom att använda BFS. BFS-implementering börjar från källan, det vill säga webbsidan, och sedan besöker alla länkar från den källan .
- Navigationssystem: BFS kan hjälpa till att hitta alla angränsande platser från huvud- eller källplatsen.
- Nätverkssändning ing: Ett sändningspaket styrs av BFS-algoritmen för att hitta och nå alla noder det har adressen till.
Sammanfattning
- En grafgenomgång är en unik process som kräver att algoritmen besöker, kontrollerar och / eller uppdaterar varje enskild obesökt nod i en trädliknande struktur. BFS-algoritmen fungerar på en liknande princip.
- Algoritmen är användbar för att analysera noderna i en graf och konstruera den kortaste vägen att korsa genom dessa.
- Algoritmen går igenom grafen i minsta antal iterationer och på kortast möjliga tid.
- BFS väljer en enda nod (initial- eller källpunkt) i ett diagram och besöker sedan alla noder intill den valda noden. BFS får åtkomst till dessa noder en efter en.
- De besökta och markerade uppgifterna placeras i en kö av BFS. En kö fungerar först utifrån. Följaktligen raderas elementet som placeras i diagrammet först och skrivs ut som ett resultat.
- BFS-algoritmen kan aldrig fastna i en oändlig slinga.
- På grund av hög precision och robust implementering används BFS i flera verkliga lösningar som P2P-nätverk, webbcrawlers, och nätverkssändning.