Hur varierar trycket med volymförändringen under adiabatisk expansion och kompression i en idealisk gas? Denna sida är en bilaga till vår diskussion om ljud. Luft vid atmosfärstryck är en nästan idealisk gas och ljudöverföring i luft är nära adiabatisk för normala frekvenser och överföringsavstånd. (Vi återgår till detta antagande nedan.)
Den första lagen om termodynamik relaterar till förändringen av den inre energin dU till det arbete dW som utförs av ett system och värmen dQ som läggs till den.
dU = dQ – dW
Per definition, i en adiabatisk process, värmeväxlade dQ = 0. Att byta ut detta i den första lagen och ordna om ger
0 = dQ = dU + dW
Den andra termen är enkel: arbetet utfört dW när ett system ändrar volymen V med dV är PdV.
Den första termen kan vara relaterad till den specifika värmen, som definieras som den tillsatta värmen per temperaturförändring per mol substans. Om vi adderar värme vid konstant volym expanderar inte gasen och fungerar inte så. Så tillsatt värme ökar den inre energin U. Så det följer den definitionen att den specifika värmen vid konstant volym är ![]() , där n är antalet mol. Därav
, där n är antalet mol. Därav
Nu är tillståndsekvationen för en idealgas
nRT = PV ( ii)
där R är gaskonstanten. Att ta derivat ger
Vi kan nu kombinera ekvationer (i) och (iii) för att eliminera T. (i) och (ii) ge respektive uttryck för ncv dT:
Samling av PdV- och VdP-termer ger
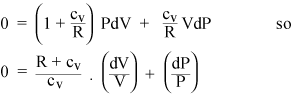
Om gasen nu är idealisk är dess inre energi all kinetisk, så den interna energin U beror bara på T. Från tillståndsekvationen för en idealgas (ii) kan vi beräkna arbetet dW utfört vid konstant tryck: det är bara PdV = nRdT. Så om vi adderar värme till en gas vid konstant tryck, måste vi extra värma RdT för varje mol gas, utöver värmen som vi borde behöva tillsätta vid konstant volym. Så den specifika värmen för en idealgas vid konstant tryck är bara cP = cv + R. Förhållandet mellan specifika värmar ges en standardsymbol:
. Så vi har
(iv)
Detta är huvudresultatet som vi behöver för att diskutera ljudvågor: vi har just visat att den proportionella tryckförändringen är – γ gånger den proportionella förändringen i volym eller γ gånger den proportionella förändringen i densitet.
Låt oss dock inte stanna här, för vi är bara några rader från ett viktigt resultat. Vi vet att d (ln x) = dx / x (se kalkyl för ett bevis). Så vi kan skriva föregående ekvation som
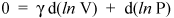
och ordna om det för att ge
(v)
Därav för en adiabatisk process i en idealgas,
. (vi)
Vid eftertanke är du överens om att cP > cV: At konstant volym, alla th värmen du sätter in går till att öka den inre energin och därmed höja temperaturen. Vid konstant tryck måste du inte bara lägga in värmen som höjer den inre energin, utan också en mängd värme som motsvarar det arbete som utförts när systemet genomgår värmeutvidgning. För luft är γ cirka 1,4.
Naturligtvis kan vi nu ersätta till (vi) från tillståndsekvationen (ii) för att se hur P och T eller T och V är relaterade till en adiabatisk process.
När är ljud adiabatiskt?
Vi nämnde ovan att ”ljudöverföring i luft är nära adiabatisk för normala frekvenser och överföringsavstånd”. När misslyckas detta? Vid tryckmaxima i en ljudvåg är temperaturen hög. Så vi förväntar oss att viss värme kommer att diffundera till närliggande tryckminima. Naturligtvis finns det inte mycket tid för värme att sprida en halv våglängd under en halv period av en ljudvåg. Tiden det tar för värme att diffundera går emellertid som avståndets kvadrat. Så denna process är mindre försumbar för höga frekvenser, eftersom den kortare halvvåglängden mer än kompenserar för den kortare halvperioden. Denna diffusion tar mekanisk energi ur vågen, särskilt vid höga frekvenser, och effekten ökar med överföringsavståndet.Av denna anledning (och ibland andra) är avlägsna ljud inte bara mindre höga utan också mindre ljusa än nära.