Förhållandet mellan tryck och volym: Boyles lag
När trycket på en gas ökar minskar gasvolymen eftersom gaspartiklarna tvingas närmare varandra. Omvänt, när trycket på en gas minskar, ökar gasvolymen eftersom gaspartiklar kan nu röra sig längre ifrån varandra. Väderballonger blir större när de stiger genom atmosfären till områden med lägre tryck eftersom gasvolymen har ökat, det vill säga den atmosfäriska gasen utövar mindre tryck på ballongens yta, så inre gas expanderar tills det inre och yttre trycket är lika.
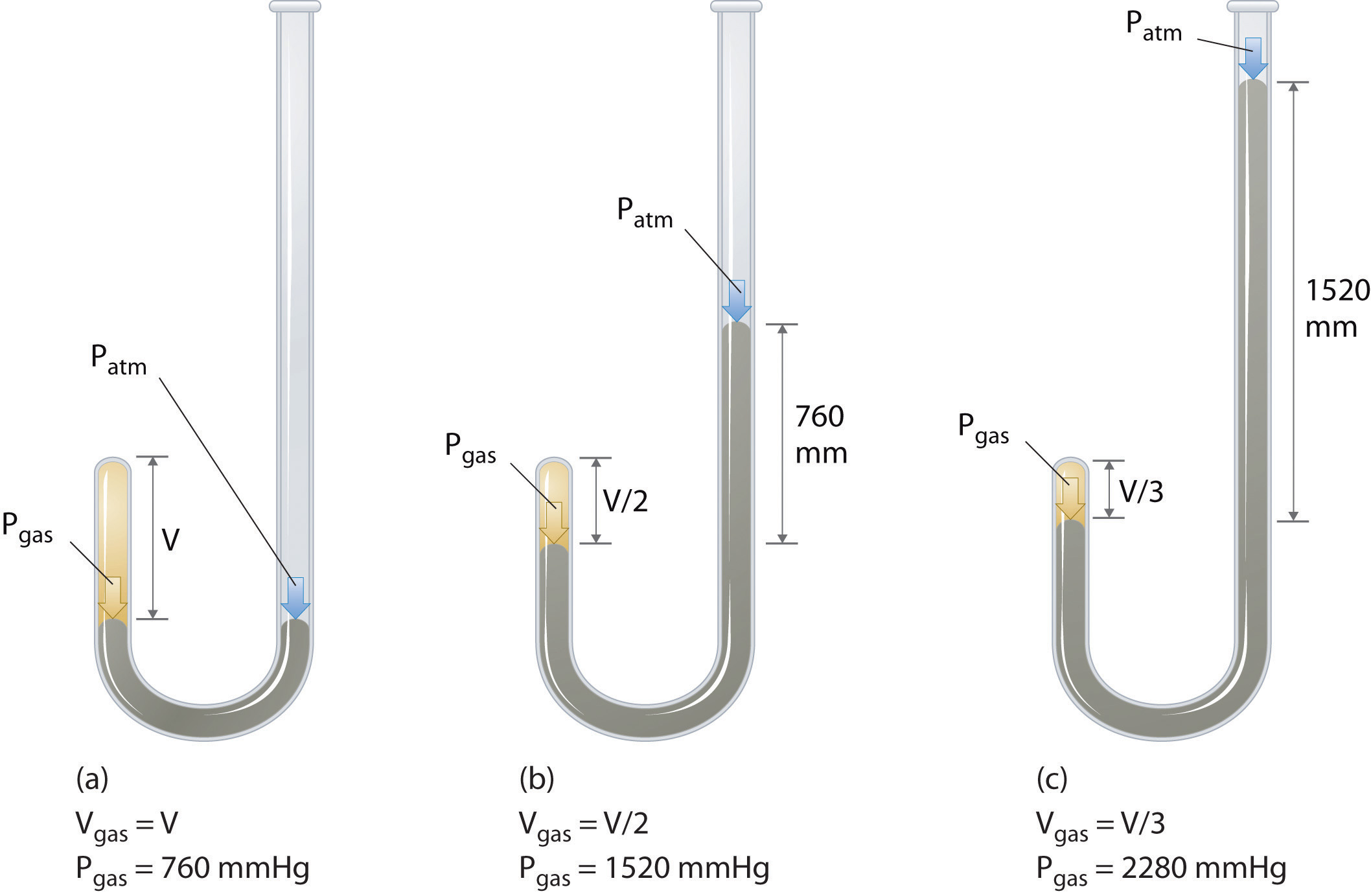
Den irländska kemisten Robert Boyle (1627–1691) genomförde några av de tidigaste experimenten som bestämde det kvantitativa sambandet mellan trycket och volymen av en gas. Boyle använde ett J-format rör delvis fyllt med kvicksilver, som visas i figur \ (\ PageIndex {1} \). I dessa experiment fångas en liten mängd gas eller luft ovanför kvicksilverkolonnen och dess volym mäts vid atmosfärstryck och konstant temperatur. Mer kvicksilver hälls sedan i den öppna armen för att öka trycket på gasprovet. Trycket på gasen är atmosfärstryck plus skillnaden i kvicksilverkolonnernas höjder och den resulterande volymen mäts. Denna process upprepas tills antingen det inte finns mer utrymme i den öppna armen eller så att gasvolymen är för liten för att mätas exakt. Data som från ett av Boyles egna experiment kan plottas på flera sätt (Figur \ (\ PageIndex {2} \)). Ett enkelt diagram av \ (V \) kontra \ (P \) ger en kurva som kallas en hyperbol och avslöjar ett omvänt förhållande mellan tryck och volym: när trycket fördubblas minskar volymen med en faktor två. Detta förhållande mellan de två storheterna beskrivs enligt följande:
\
Att dela båda sidor med \ (P \) ger en ekvation som illustrerar det inversa förhållandet mellan \ (P \) och \ (V \):
\
eller
\
där ∝-symbolen läses ”är proportionell mot.” En plot av V kontra 1 / P är alltså en rak linje vars lutning är lika med konstanten i ekvationer \ (\ ref {10.3.1} \) och \ (\ ref {10.3.3} \). Delar båda sidor av Ekvation \ (\ ref {10.3.1} \) med V istället för P ger ett liknande förhållande mellan P och 1 / V. Det numeriska värdet på konstanten beror på mängden gas som används i experimentet och på temperaturen vid vilken experimenten utförs. Detta förhållande mellan tryck och volym är känt som Boyles lag, efter dess upptäckare, och kan anges på följande sätt: Vid konstant temperatur är volymen för en fast mängd gas en omvänt proportionell mot dess tryck. lag i praktiken visas i figur \ (\ PageIndex {2} \).
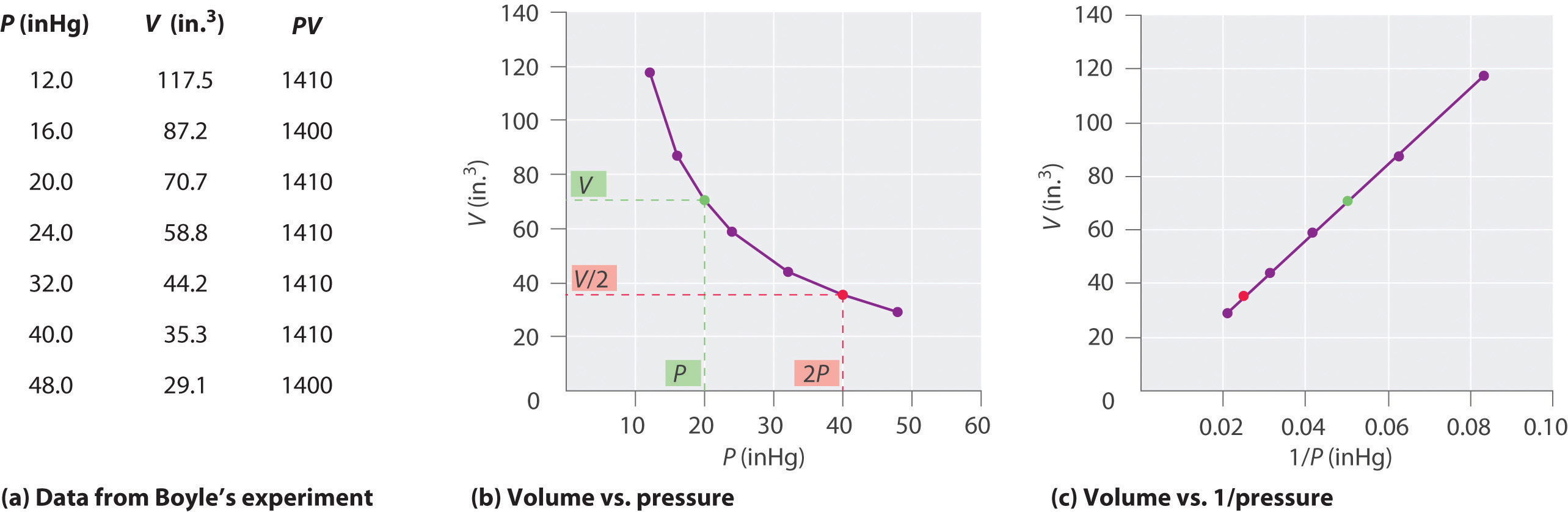
Vid konstant temperatur är volymen för en fast mängd av en gas omvänt proportionell mot dess tryck