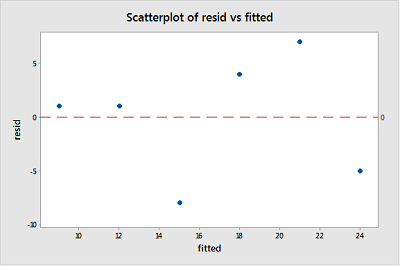
När du utför en restanalys är en ”residuals versus fit-plot” den mest skapade plot. Det är ett spridningsdiagram över rester på y-axeln och anpassade värden (uppskattade svar) på x-axeln. Diagrammet används för att upptäcka icke-linjäritet, ojämna felvariationer och outliers.
Låt oss titta på ett exempel för att se hur en ”välskött” restdiagram ser ut. Vissa forskare (Urbano- Marquez, et al., 1989) var intresserade av att bestämma huruvida alkoholkonsumtion var linjärt relaterad till muskelstyrka. Forskarna mätte den totala livskonsumtionen av alkohol (x) i ett slumpmässigt urval av n = 50 alkoholister. styrkan (y) hos deltoidmuskeln i varje persons icke-dominerande arm. En anpassad linjediagram över de resulterande data, (alcoholarm.txt), ser ut som:
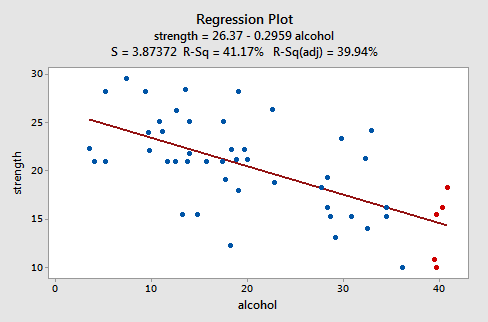
Handlingen antyder att det finns ett minskande linjärt samband mellan alkohol och armstyrka. Det antyder också att det inte finns några ovanliga datapunkter i datamängden. Och det illustrerar att variationen runt den uppskattade regressionslinjen är konstant, vilket antyder att antagandet om lika felvariationer är rimligt.
Här ser motsvarande rester kontra passform för datauppsättningen ut enkel linjär regressionsmodell med armstyrka som respons och alkoholkonsumtionsnivå som prediktor:
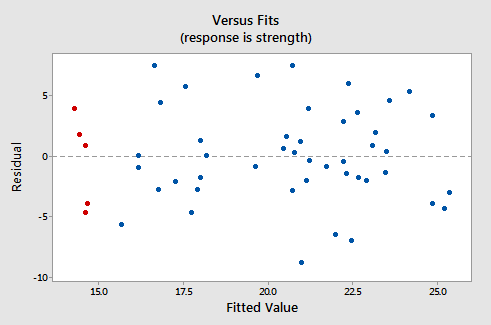
Observera att, som definierat, resterna visas på y-axeln och de monterade värdena visas på x-axeln. Du borde kunna se tillbaka på spridningsdiagrammet för datan och se hur datapunkterna där motsvarar datapunkterna i den återstående kontra passformen här. Om du har problem med att göra det, titta på de fem datapunkterna i den ursprungliga spridningsdiagrammet som visas i rött. Observera att det förutspådda svaret (anpassat värde) för dessa män (vars alkoholkonsumtion är cirka 40) är cirka 14 Observera också mönstret där de fem datapunkterna avviker från den uppskattade regressionslinjen.
Titta nu på hur och var dessa fem datapunkter visas i diagrammet för resterande kontra passform. Deras anpassade värde är cirka 14 och deras avvikelse från den kvarvarande = 0-raden delar samma mönster som deras avvikelse från den uppskattade regressionslinjen. Ser du anslutningen? Alla datapunkter som faller direkt på den uppskattade regressionslinjen har en rest på 0. Därför är den återstående = 0-linjen motsvarar den uppskattade regressionslinjen.
Denna plot är ett klassiskt exempel på en väluppfostrad rest vs. kontraktsdiagram. Här är egenskaperna hos en väluppfostrad rest vs. passar-plot och vad de föreslå om lämpligheten av det enkla e linjär regressionsmodell:
- Resterna ”studsar slumpmässigt” runt 0-raden. Detta antyder att antagandet att förhållandet är linjärt är rimligt.
- Resterna bildar ungefär ett ”horisontellt band” runt 0-linjen. Detta antyder att avvikelserna i felvillkoren är lika.
- Ingen rest ”sticker ut” från det grundläggande slumpmässiga mönstret för restprodukter. Detta tyder på att det inte finns några outliers.
I allmänhet vill du att dina kvarvarande kontra plottrar ska se ut ungefär som ovanstående plot. Glöm inte att tolkningen av dessa tomter är subjektiv. Min erfarenhet har varit att studenter som lär sig restanalys för första gången tenderar att övertolka dessa tomter och ser på varje vridning och vändning som något som är potentiellt besvärligt. Du vill särskilt var försiktig med att lägga för mycket vikt på kvarvarande kontra tomter baserat på små datamängder. Ibland är datamängderna alldeles för små för att göra tolkningen av en rest vs. Oroa dig inte! Du lär dig – med övning – hur man ”läser” dessa diagram.