Antag att luft pumpas ner i ett slätt runt rör, som har en konstant diameter förutom en sektion i mitten där röret smalnar ner till hälften av diametern, bredda sedan ut igen. Antag att alla förändringar i diameter sker smidigt och luften strömmar stadigt ner röret, utan virvlar eller turbulens.
Träning
var i röret förväntar du dig trycket att vara störst?
Svar
De flesta frågade detta för första gången förutspår att trycket kommer att vara störst i rörets smala del. Men faktiskt, om vi faktiskt gör experimentet, genom att sätta tryckmätare vid olika punkter längs röret, finner vi, mot intuitivt, att lufttrycket är lägst där luften rör sig snabbast!

För att se hur detta kan vara kommer vi att tillämpa teknikerna vi utvecklade för att hitta hur trycket varierade i en stationär vätska. Hur vi gjorde det, kom ihåg, genom att rita ett frikroppsdiagram för en liten vätskeflaska. Eftersom den här lilla cylindern var i vila var den totala kraften på den noll, så nettotrycket balanserade vikten. Tänk nu på en stadigt rörlig vätska. Det är bra att visualisera flödet genom att rita in strömlinjer, linjer så att deras riktning är den riktning vätskan rör sig i vid varje punkt.

Egentligen berättar dessa strömlinjer dig inte bara i vilken riktning vätskan rör sig, utan ger också en uppfattning om hastigheten – där de kommer närmare varandra måste vätskan röra sig snabbare, eftersom samma mängd vätska flyter genom en smalare region. Föreställ dig nu en luftcylinder som rör sig längs röret, dess axel parallell med strömlinjen. Uppenbarligen måste den påskyndas när den kommer in i den smala delen av röret – eftersom samma mängd luft strömmar genom den smala delen som den breda delen, måste den gå snabbare.
Men om den lilla delen Om vätskecylindern accelererar måste den påverkas av en kraft som skjuter den bakifrån.
Dess vikt är irrelevant här, eftersom den rör sig horisontellt. Därför är den enda kraften som verkar på det trycket, och vi måste dra slutsatsen att trycket vid dess baksida är större än trycket på dess front. Därför måste trycket sjunka när det kommer in i den smala delen. För att klargöra vad som händer, drar vi en ganska stor cylinder:
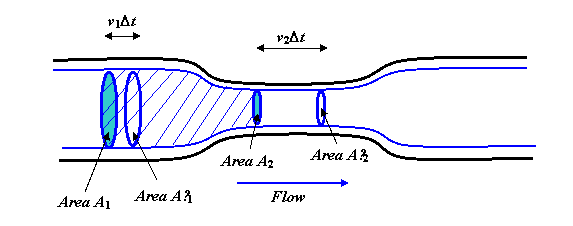
Vätskan flyter stadigt och jämnt längs röret. De tjocka blå linjerna är strömlinjeformade, i själva verket kan du tänka dig att rotera hela diagrammet runt den centrala axeln för att få en tredimensionell bild, och de blå linjerna skulle bli en cylinder, med en smalare ”hals” -sektion, som ekar formen på rör.
Tänk nu på vätskekroppen inom de strömlinjer som visas, och avgränsas i de två ändarna av de cirkulära områdena A1 och A2. Flödeshastigheten för vätska över A1 måste vara densamma som hastigheten för flöde över A2, för att i stadig flöde inte kan vätska i mitten (eller tömma därifrån heller). Volymen som flyter över A1 på en sekund är v1A1. (För att se detta, föreställ dig ett långt rakt rör utan en smal Om vätskan flyter med, säg 3 meter per sekund, kommer all vätska som var inom 3 meter från området A1 på uppströmsidan på en sekund att ha runnit igenom.)
Så, flöde över A1 är lika med flöde över A2, \
(Fotnot: Det är kanske värt att nämna att vi implicit antar veloci ty är densamma vid alla punkter i område A1. Varje riktig vätska har viss viskositet (friktion) och kommer att röra sig långsammare nära rörets sidor än i mitten. Vi kommer att diskutera detta senare. För närvarande betraktar vi en ”ideal” vätska, den term som används när man ignorerar viskositeten. Faktum är att resultatet vi får är ok – vi kunde ha tagit ett litet område A1 långt bort från sidorna så att hastigheten skulle ha varit detsamma för hela området, men det skulle ha gett ett mycket mindre tydligt diagram.)
Vi är nu redo att undersöka ökningen av vätskans kinetiska energi när den snabbar upp i den smala delen, och förstå hur tryckdifferensen gjorde det arbete som var nödvändigt för att påskynda den.
\
Den enda möjliga källan för denna energiökning är det arbete som utförs genom tryck för att trycka vätskan in i den smala delen.
\
Så detta är arbete som görs på vår vätskebitar genom att vätskan skjuter den bakifrån – men det är inte slutet på berättelsen, för vår bit av själva vätskan fungerar för att trycka vätskan framför den, så för att hitta den totala ökningen av vår bit energi måste vi subtrahera det externa arbete som det gör.Det vill säga, det totala arbetet som utförs av tryck på vår vätska är
\
att komma ihåg att \ (A_1v_1 = A_2v_2 \).
Detta utförda arbete måste vara förändringen i kinetisk energi, så
\
från vilken
\
Detta är Bernoullis ekvation.
\.
Bidragsgivare och attribut
- Michael Fowler (Beams Professor, Department of Physics, University of Virginia)