A soma é o resultado de uma adição. Por exemplo, adicionar 1, 2, 3 e 4 dá a soma 10, escrita
 |
(1)
|
Os números que estão sendo somados são chamados de adendos ou, às vezes, de soma. A operação de soma também pode ser indicada usando um sigma maiúsculo com limites superior e inferior escritos acima e abaixo, e o índice indicado abaixo. Por exemplo, a soma acima pode ser escrita
 |
(2)
|
O a soma de uma lista de números é implementada como Total.
Uma soma
 |
(3)
|
em que cada termo 
é fornecido por alguma regra fixa (ou seja, 
é um poço seqüência definida) é chamada de série (finita), e se o número de termos 
for infinito, a soma é chamada de série infinita (ou frequentemente apenas uma “série”). Uma soma da forma
 |
(4)
|
é chamada de série geométrica .
As condições para convergência de uma série podem ser determinadas na linguagem Wolfram usando SumConvergence.
A soma geral finita da potência
 |
(5)
|
pode ser dado pela expressão
 |
(6)
|
que é equivalente à fórmula de Faulhaber, onde a notação 
significa a quantidade em questão é levantada com a potência apropriada 
e todos os termos da forma 
são substituídos pelos correspondentes Números de Bernoulli 
.
Uma identidade divertida devida a J. Ziegenbein (pers. comm., 19 de junho de 2002) segue a partir da identidade
 |
(7)
|
que pode ser escrito
 |
(8)
|
Portanto, 
, por exemplo, pode ser escrito nas formas equivalentes
 |
 |
 |
(9)
|
 |
 |
 |
(10)
|
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
e assim por diante.
O teorema de Nicômaco fornece uma expressão curiosa para a soma das potências 
.
As somas especiais incluem
 |
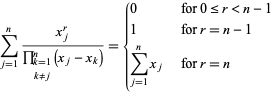(13)
|
e
 |
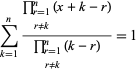(14)
|
Para minimizar a soma de um conjunto de quadrados de números 
sobre um determinado número 
 |
 |
 |
(15 )
|
 |
 |
 |
(16)
|
tire a derivada.
 |
(17)
|
A resolução de 
dá
 |
(18)
|
então 
é minimizado quando 
é definido como o significa.