Como a pressão varia com a mudança de volume durante a expansão e compressão adiabática em um gás ideal? Esta página é um apêndice de nossa discussão sobre som. O ar à pressão atmosférica é um gás quase ideal e a transmissão do som no ar é quase adiabática para frequências normais e distâncias de transmissão. (Retornamos a essa suposição abaixo.)
A primeira lei da termodinâmica relaciona a mudança na energia interna dU ao trabalho dW feito por um sistema e ao calor dQ adicionado a ele.
dU = dQ – dW
Por definição, em um processo adiabático, o calor trocado dQ = 0. Substituir isso na primeira lei e reorganizar dá
0 = dQ = dU + dW
O segundo termo é fácil: o trabalho feito dW quando um sistema muda seu volume V por dV é PdV.
O primeiro termo pode estar relacionado ao calor específico, que é definido como o calor adicionado por unidade de mudança de temperatura por mol de substância. Se adicionarmos calor em volume constante, o gás não se expande e, portanto, não funciona. Portanto, o calor adicionado aumenta a energia interna U. Portanto, segue-se essa definição que o calor específico em volume constante é ![]() , onde n é o número de moles. Portanto,
, onde n é o número de moles. Portanto,
Agora, a equação de estado de um gás ideal é
nRT = PV ( ii)
onde R é a constante do gás. Tirar os derivados dá
Podemos agora combinar as equações (i) e (iii) para eliminar T. (i) e (ii) forneça respectivamente essas expressões para ncv dT:
A coleta dos termos PdV e VdP dá
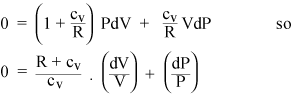
Agora, se o gás é ideal, sua energia interna é toda cinética, então a energia interna U depende apenas de T. A partir da equação de estado de um gás ideal (ii), podemos calcular o trabalho dW feito a pressão constante: é apenas PdV = nRdT. Portanto, se adicionarmos calor a um gás a pressão constante, temos que adicionar calor extra para cada mol de gás, além do calor que deveríamos ter que adicionar em volume constante. Portanto, o calor específico de um gás ideal a pressão constante é apenas cP = cv + R. A proporção de calores específicos recebe um símbolo padrão:
. Portanto, temos
(iv)
Este é o resultado principal de que precisamos para discutir as ondas sonoras: acabamos de mostrar que a mudança proporcional na pressão é – γ vezes a mudança proporcional no volume ou γ vezes a mudança proporcional na densidade.
Não vamos parar por aqui, entretanto, porque estamos a apenas algumas linhas de um resultado importante. Sabemos que d (ln x) = dx / x (veja cálculo para uma prova). Portanto, podemos escrever a equação anterior como
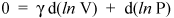
e reorganize-o para fornecer
(v)
Portanto, para um processo adiabático em um gás ideal,
. (vi)
Pensando bem, você “concordará que cP > cV: Em volume constante, todo o O calor que você coloca vai para aumentar a energia interna e, assim, aumentar a temperatura. Com pressão constante, é necessário colocar não apenas o calor que aumenta a energia interna, mas também uma quantidade de calor igual ao trabalho realizado quando o sistema sofre expansão térmica. Para o ar, γ é cerca de 1,4.
Claro, podemos agora substituir em (vi) a partir da equação de estado (ii) para ver como P e T ou T e V estão relacionados para um processo adiabático.
Quando o som é adiabático?
Mencionamos acima que “a transmissão do som no ar é quase adiabática para frequências normais e distâncias de transmissão”. Quando isso falha? Nos máximos de pressão em uma onda sonora, a temperatura está alta. Portanto, esperamos que algum calor se difunda para os mínimos de pressão vizinhos. É claro que, em meio período de uma onda sonora, não há muito tempo para o calor se difundir em meio comprimento de onda. No entanto, o tempo que leva para o calor se difundir é o quadrado da distância. Portanto, esse processo é menos desprezível para altas frequências, porque a metade do comprimento de onda mais curta mais do que compensa a metade do período mais curto. Essa difusão retira energia mecânica da onda, especialmente em altas frequências, e o efeito aumenta com a distância de transmissão.Por esta razão (e às vezes outras), sons distantes não são apenas menos altos, mas também menos brilhantes do que os próximos.