Suponha que o ar esteja sendo bombeado por um tubo redondo liso, que tem um diâmetro constante, exceto por uma seção no meio onde o tubo se estreita até a metade do diâmetro, depois se alarga novamente. Suponha que todas as mudanças no diâmetro ocorram suavemente, e o ar flua continuamente para baixo do tubo, sem redemoinhos ou turbulência.
Exercício
onde no tubo você espera a pressão deve ser maior?
Resposta
A maioria das pessoas que perguntou isso pela primeira vez prevê que a pressão será maior na parte estreita do tubo. Mas, na verdade, se realmente fizermos o experimento, colocando medidores de pressão em vários pontos ao longo do tubo, descobriremos, contra a intuição, que a pressão do ar é mais baixa onde o ar se move mais rápido!

Para ver como isso poderia ser, aplicaremos as técnicas que desenvolvemos para descobrir como a pressão varia em um fluido estacionário. A maneira como fizemos isso, lembre-se, foi desenhando um diagrama de corpo livre para um pequeno cilindro de fluido. Como esse pequeno cilindro estava em repouso, a força total sobre ele era zero, então a pressão líquida equilibrava o peso. Agora considere um fluido em movimento constante. É útil visualizar o fluxo desenhando em linhas aerodinâmicas, linhas tais que sua direção seja a direção em que o fluido está se movendo em cada ponto.

Na verdade, essas linhas aerodinâmicas não apenas informam a direção em que o fluido está se movendo, mas também dão uma ideia da velocidade – onde eles se aproximam, o fluido deve estar se movendo mais rápido, porque a mesma quantidade de fluido está fluindo através de uma região mais estreita. Imagine agora um cilindro de ar movendo-se ao longo do tubo, seu eixo paralelo à linha do fluxo. Obviamente, ele deve acelerar ao entrar na parte estreita do tubo – uma vez que a mesma quantidade de ar está fluindo através da parte estreita e da parte larga, ele deve estar indo mais rápido.
Mas se o pequeno cilindro de fluido está acelerando, ele deve ser acionado por uma força que o empurra por trás.
Seu peso é irrelevante aqui, pois ele está se movendo horizontalmente. Portanto, a única força que age sobre ele é a pressão, e temos que concluir que a pressão em sua parte traseira é maior do que a pressão em sua parte frontal. Portanto, a pressão deve estar caindo ao entrar na parte estreita. Para deixar mais claro o que está acontecendo, desenharemos um cilindro bastante grande:
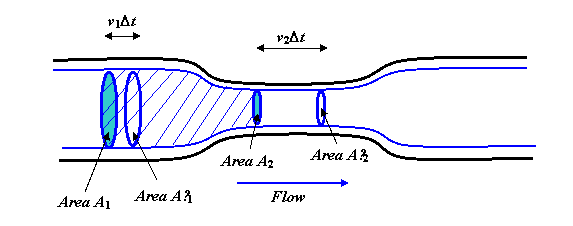
O fluido está fluindo de forma constante e suave ao longo o cano. As linhas azuis grossas são linhas aerodinâmicas, na verdade, você deve imaginar girar todo o diagrama sobre o eixo central para obter uma imagem tridimensional, e as linhas azuis se tornariam um cilindro, com uma seção de “pescoço” mais estreita, ecoando a forma do tubo.
Agora, considere o corpo de fluido dentro das linhas de fluxo mostradas e coberto nas duas extremidades pelas áreas circulares A1 e A2. A taxa de fluxo de fluido através de A1 deve ser igual à taxa de fluir através de A2, porque em fluxo constante o fluido não pode se acumular no meio (ou se esgotar de lá também). O volume que flui através de A1 em um segundo é v1A1. (Para ver isso, imagine um tubo longo e reto sem um tubo estreito parte. Se o fluido estiver fluindo a, digamos, 3 metros por segundo, então em um segundo todo o fluido que estava dentro de 3 metros da área A1 no lado a montante terá passado.)
Então, fluxo em A1 é igual a fluxo em A2, \
(Nota de rodapé: talvez valha a pena mencionar que estamos assumindo implicitamente a velocidade ty é o mesmo em todos os pontos da área A1. Qualquer fluido real tem alguma viscosidade (atrito) e se moverá mais lentamente próximo às laterais do tubo do que no meio. Discutiremos isso mais tarde. Por enquanto, consideramos um fluido “ideal”, o termo usado quando se ignora a viscosidade. Na verdade, o resultado que derivamos está ok – poderíamos ter tomado uma pequena área A1 longe dos lados, de modo que a velocidade teria sido o mesmo para toda a área, mas isso teria dado um diagrama muito menos claro.)
Agora estamos prontos para examinar o aumento da energia cinética do fluido conforme ele acelera na parte estreita, e entender como a diferença de pressão fez o trabalho necessário para acelerá-la.
\
A única fonte possível para esse aumento de energia é o trabalho feito pela pressão ao empurrar o fluido para dentro a parte estreita.
\
Portanto, este é um trabalho feito em nosso pedaço de fluido pelo fluido empurrando-o por trás – mas esse não é o fim da história, porque nosso pedaço de o próprio fluido funciona empurrando o fluido à sua frente; portanto, para encontrar o aumento total na energia do nosso pedaço, devemos subtrair o trabalho externo que ele realiza.Ou seja, o trabalho total realizado por pressão em nosso fluido é
\
lembrando que \ (A_1v_1 = A_2v_2 \).
Este trabalho realizado deve ser igual a mudança na energia cinética, então
\
a partir da qual
\
Esta é a equação de Bernoulli.
\.
Contribuidores e atribuições
- Michael Fowler (Professor Beams, Departamento de Física, Universidade da Virgínia)