 |
원은 쉽게 만들 수 있습니다. 중심점에서 “반지름”떨어져있는 기타 : 모든 지점이 중심에서 같은 거리에 있습니다. |

직접 그릴 수 있습니다
보드에 핀을 넣고 그 주위에 줄 고리를 놓고 삽입 루프에 연필. 끈을 늘인 상태로 원을 그립니다!
연습
점을 드래그하여 반경과 원주가 어떻게 변하는 지 확인하세요.
( 일정한 반경!)
반지름, 지름 및 원주

반경은 중심에서 바깥쪽으로의 거리입니다.
직경은 중심을 통해 원을 가로 질러 직선으로 이동합니다.
둘레는 거리입니다. 여기에 정말 멋진 것이 있습니다.
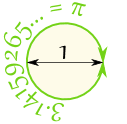
원주를 지름으로 나누면 3.141592654 …
숫자 π (Pi)
|
따라서 지름이 1 일 때 둘레는 3.141592654 … |
 |
우리는 다음과 같이 말할 수 있습니다.
원주 = π × 지름
예 : 지름이 100m 인 원 주위를 걷습니다. 얼마나 멀리 걸었습니까?
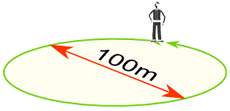
걸은 거리 = 둘레 = π × 100m
= 314m (가장 가까운 m까지)
또한 지름은 반지름의 두 배입니다.
직경 = 2 × 반지름
또한 이것이 사실입니다.
원주 = 2 × π × 반경
요약 :
| × 2 | × π |
| |
|
| 반지름 | 직경 | 원주 |
기억하기
단어의 길이는 기억하는 데 도움이 될 수 있습니다.
- 반경 가장 짧은 단어이고 짧습니다. est measure
- 지름이 더 깁니다
- 원주가 가장 깁니다
정의
 |
원은 평면 모양 (2 차원)이므로 : |
원 : 중심에서 고정 된 거리에있는 평면의 모든 점 집합입니다.
Area

원의 면적은 반지름 제곱의 π 곱입니다. 서면 :
A = π r2
어디
- A는 면적
- r은 반경
“파이 제곱”을 기억하는 데 도움이되는 방법 (파이는 일반적으로 원형이지만) :

예 : 반경 1.2m 인 원의 면적은 얼마입니까?
또는 지름 사용 :

A = (π / 4) × D2
정사각형과 비교 한 면적

원은 너비가 비슷한 정사각형 면적의 약 80 %를 차지합니다.
실제 값은 (π / 4) = 0.785398입니다. . = 78.5398 … %
그리고 흥미로운 점 :
선으로 원 영역보기
이름
사람들이 수천 년 동안 연구 서클에 특별한 이름이 생겼습니다.
아무도 “원의 한쪽에서 시작하여 중앙을지나 다른 쪽에서 끝나는 선”이라고 말하고 싶어하지 않습니다. “직경”이라고 말하세요.
다음은 가장 일반적인 특수 이름입니다.
선

원이 지나갈 때”그냥 닿는 “선을 접선이라고합니다.
원을 두 점에서 자르는 선을 시컨트.
원의 원주상의 한 지점에서 다른 지점으로가는 선분을 코드라고합니다.
중심을 통과하는 지름을 지름이라고합니다.
원주의 일부를 호라고합니다.

슬라이스
원에는 두 개의 주요 “슬라이스”가 있습니다.
“피자”슬라이스를 섹터라고합니다.
코드로 만든 슬라이스를 세그먼트라고합니다.
공통 섹터
사분면과 반원은 두 가지 특수한 유형의 섹터입니다.

원의 사분면을 사분면이라고합니다.

반원을 반원이라고합니다.
내부 및 외부

원에는 내부가 있습니다. 그리고 외부 (물론!). 하지만 우리가 원 위에있을 수 있기 때문에 “켜짐”이 있습니다.
예 : “A”는 원 밖에 있고 “B”는 원 안에, “C”는 원 위에 있습니다. .

타원
원은 타원의 “특별한 경우”입니다.