 |
Un círculo es fácil de hacer: Dibuja una curva que esté a un «radio» de distancia Y así: Todos los puntos están a la misma distancia del centro. |

Puedes dibujarlo tú mismo
Pon un alfiler en un tablero, coloca un lazo de cuerda alrededor e inserta un lápiz en el bucle. ¡Mantenga la cuerda estirada y dibuje el círculo!
Juega con él
Intenta arrastrar el punto para ver cómo cambian el radio y la circunferencia.
(Mira si puedes mantener ¡un radio constante!)
Radio, diámetro y circunferencia

El radio es la distancia desde el centro hacia afuera.
El diámetro va recto a través del círculo, a través del centro.
La circunferencia es la distancia una vez alrededor del círculo.
Y aquí está lo realmente genial:
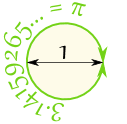
Cuando dividimos la circunferencia por el diámetro obtenemos 3,141592654 …
que es el número π (Pi)
|
Entonces, cuando el diámetro es 1, la circunferencia es 3.141592654 … |
 |
Podemos decir:
Circunferencia = π × Diámetro
Ejemplo: Caminas alrededor de un círculo que tiene un diámetro de 100 m, ¿cuánto has caminado?
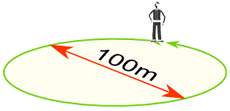
Distancia caminada = Circunferencia = π × 100 m
= 314 m (al metro más cercano)
También tenga en cuenta que el diámetro es el doble del radio:
Diámetro = 2 × Radio
Y esto también es cierto:
Circunferencia = 2 × π × Radio
En resumen:
| × 2 | × π |
| |
|
| Radio | Diámetro | Circunferencia |
Recordando
La longitud de las palabras puede ayudarlo a recordar:
- Radio es la palabra más corta y corta medida est
- El diámetro es más largo
- La circunferencia es la más larga
Definición
 |
El círculo es una forma plana (bidimensional), entonces: |
Círculo: el conjunto de todos los puntos en un plano que están a una distancia fija de un centro.
Área

El área de un círculo es π veces el radio al cuadrado, que es escrito:
A = π r2
Donde
- A es el área
- r es el radio
Para ayudarte a recordar que piensas en «Los pasteles son cuadrados» (aunque los pasteles suelen ser redondos):

Ejemplo: ¿Cuál es el área de un círculo con un radio de 1.2 m?
O, usando el Diámetro:

A = (π / 4) × D2
Área comparada con un cuadrado

Un círculo tiene aproximadamente el 80% del área de un cuadrado de ancho similar.
El valor real es (π / 4) = 0.785398 .. . = 78.5398 …%
Y algo interesante para ti:
Ver el área del círculo por líneas
Nombres
Porque la gente ha círculos estudiados durante miles de años han surgido nombres especiales.
Nadie quiere decir «esa línea que comienza en un lado del círculo, pasa por el centro y termina en el otro lado» cuando puede diga «Diámetro».
Estos son los nombres especiales más comunes:
Líneas

Una línea que» simplemente toca «el círculo cuando pasa se llama Tangente.
Una línea que corta el círculo en dos puntos se llama Secante.
Un segmento de línea que va de un punto a otro en la circunferencia del círculo se llama acorde.
Si pasa a través del centro se llama Diámetro.
Y una parte de la circunferencia se llama Arco.

Rebanadas
Hay dos «sectores» principales de un círculo.
La porción de «pizza» se llama Sector.
Y la porción hecha por un acorde se llama Segmento.
Sectores comunes
El cuadrante y el semicírculo son dos tipos especiales de sector:

Un cuarto de círculo se llama Cuadrante.

El medio círculo se denomina semicírculo.
Interior y exterior

Un círculo tiene un interior y un exterior (¡por supuesto!). Pero también tiene un «activado», porque podríamos estar justo en el círculo.
Ejemplo: «A» está fuera del círculo, «B» está dentro del círculo y «C» está en el círculo. .

Elipse
Un círculo es un «caso especial» de una elipse.