 |
Ein Kreis ist einfach zu erstellen: Zeichnen Sie eine Kurve, die „Radius“ von einem Mittelpunkt entfernt ist. Und so: Alle Punkte haben den gleichen Abstand vom Zentrum. |

Sie können es selbst zeichnen
Stecken Sie einen Stift in ein Brett, legen Sie eine Schnurschleife darum und fügen Sie es ein ein Bleistift in die Schleife. Halten Sie die Zeichenfolge gestreckt und zeichnen Sie den Kreis!
Spielen Sie damit
Ziehen Sie den Punkt, um zu sehen, wie sich Radius und Umfang ändern.
(Sehen Sie, ob Sie ihn behalten können ein konstanter Radius!)
Radius, Durchmesser und Umfang

Der Radius ist der Abstand von der Mitte nach außen.
Der Durchmesser verläuft gerade über den Kreis durch die Mitte.
Der Umfang ist der Abstand einmal um den Kreis herum.
Und hier ist das wirklich Coole:
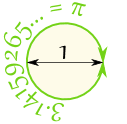
Wenn wir den Umfang durch den Durchmesser teilen, erhalten wir 3.141592654 …
das ist das Zahl π (Pi)
|
Wenn also der Durchmesser 1 ist, beträgt der Umfang 3,141592654 … |
 |
Wir können sagen:
Umfang = π × Durchmesser
Beispiel: Sie gehen um einen Kreis mit einem Durchmesser von 100 m. Wie weit sind Sie gegangen?
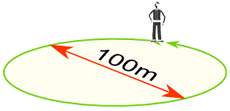
Gehstrecke = Umfang = π × 100 m
= 314 m (auf das nächste m)
Beachten Sie auch, dass der Durchmesser doppelt so groß ist wie der Radius:
Durchmesser = 2 × Radius
Dies gilt also auch:
Umfang = 2 × π × Radius
Zusammenfassend:
| × 2 | × π |
| |
|
| Radius | Durchmesser | Umfang |
Erinnern
Die Länge der Wörter kann Ihnen helfen, sich zu erinnern:
- Radius ist das kürzeste Wort und kurz est Maß
- Durchmesser ist länger
- Umfang ist der längste
Definition
 |
Der Kreis ist eine ebene Form (zweidimensional), also: |
Kreis: Die Menge aller Punkte auf einer Ebene, die einen festen Abstand von einem Zentrum haben.
Fläche

Die Fläche eines Kreises ist das π-fache des quadratischen Radius geschrieben:
A = π r2
Wobei
- A die Fläche ist
- r der Radius
Damit Sie sich besser an „Pie Are Squared“ erinnern (obwohl die Kuchen normalerweise rund sind):

Beispiel: Wie groß ist die Fläche eines Kreises mit einem Radius von 1,2 m?
Oder verwenden Sie den Durchmesser:

A = (π / 4) × D2
Fläche im Vergleich zu einem Quadrat

Ein Kreis hat ungefähr 80% der Fläche eines Quadrats ähnlicher Breite.
Der tatsächliche Wert ist (π / 4) = 0,785398. . = 78.5398 …%
Und etwas Interessantes für Sie:
Siehe Kreisbereich nach Linien
Namen
Weil Menschen haben Seit Tausenden von Jahren studierte Kreise. Spezielle Namen sind entstanden.
Niemand möchte sagen, „diese Linie, die auf einer Seite des Kreises beginnt, durch die Mitte geht und auf der anderen Seite endet“, wenn er kann Sagen Sie „Durchmesser“.
Hier sind die häufigsten Sondernamen:
Zeilen

Eine Linie, die den vorbeifahrenden Kreis“ nur berührt „, wird als Tangente bezeichnet.
Eine Linie, die den Kreis an zwei Punkten schneidet, wird aufgerufen eine Sekante.
Ein Liniensegment, das auf dem Kreisumfang von einem Punkt zum anderen verläuft, wird als Akkord bezeichnet.
Wenn es passiert Durch die Mitte wird es als Durchmesser bezeichnet.
Und ein Teil des Umfangs wird als Bogen bezeichnet.

Slices
Es gibt zwei Haupt- „Slices“ eines Kreises.
Das „Pizza“ -Schnitt wird als Sektor bezeichnet.
Und das von einem Akkord erzeugte Stück wird als Segment bezeichnet.
Gemeinsame Sektoren
Der Quadrant und der Halbkreis sind zwei spezielle Sektortypen:

Ein Viertel eines Kreises wird Quadrant genannt.

Ein halber Kreis wird als Halbkreis bezeichnet.
Innen und Außen

Ein Kreis hat eine Innenseite und eine Außenseite (natürlich!). Es hat aber auch ein „Ein“, weil wir uns direkt auf dem Kreis befinden könnten.
Beispiel: „A“ befindet sich außerhalb des Kreises, „B“ befindet sich innerhalb des Kreises und „C“ befindet sich auf dem Kreis

Ellipse
Ein Kreis ist ein „Sonderfall“ einer Ellipse.