Thevenins sætning siger, at det er muligt at forenkle ethvert lineært kredsløb, uanset hvor komplekst, til et ækvivalent kredsløb med kun en enkelt spændingskilde og seriemodstand forbundet med en belastning. Kvalifikationen af “lineær” er identisk med den, der findes i Superpositionssætningen, hvor alle de underliggende ligninger skal være lineære (ingen eksponenter eller rødder). Hvis vi har at gøre med passive komponenter (såsom modstande og senere, induktorer og kondensatorer Der er dog nogle komponenter (især visse gasudladnings- og halvlederkomponenter), som er ikke-lineære: dvs. deres modstand mod strømændringer med spænding og / eller strøm. Som sådan vil vi kalde kredsløb, der indeholder disse typer af komponenter, ikke-lineære kredsløb.
Thevenins sætning i elsystemer
Thevenins sætning er især nyttig til analyse af elsystemer og andre kredsløb, hvor en bestemt modstand i kredsløbet (kaldet “belastning ”Modstand) kan ændres, og genberegning af kredsløbet er nødvendig med hver prøveværdi af belastningsmodstand for at bestemme spændingen over den og strøm gennem den. Lad os se endnu en gang på vores eksempler på kredsløb:

Lad os antage, at vi beslutter at udpege R2 som “belastnings” -modstanden i Vi har allerede fire analysemetoder til rådighed (grenstrøm, netstrøm, Millmans teorem og superpositionssætning), der skal bruges til at bestemme spændingen over R2 og strøm gennem R2, men hver af disse metoder er tidskrævende. Forestil dig at gentage en af disse metoder igen og igen for at finde ud af, hvad der ville ske, hvis belastningsmodstanden ændredes (ændring af belastningsmodstand er meget almindeligt i elsystemer, da flere belastninger tændes og slukkes efter behov. Den samlede modstand af deres parallelle forbindelser ændres afhængigt af hvor mange der er forbundet ad gangen). Dette kan potentielt indebære en masse arbejde!
Thevenin Equivalent Circuit
Thevenins sætning gør det let ved midlertidigt at fjerne belastningsmodstanden fra oprindelige kredsløb og reducere hvad der er tilbage til en ækvivalent cir cuit sammensat af en enkelt spændingskilde og seriemodstand. Belastningsmodstanden kan derefter forbindes igen til dette “Thevenin-ækvivalente kredsløb” og beregninger udføres som om hele netværket kun var et simpelt seriekredsløb:

… efter Thevenin-konvertering..
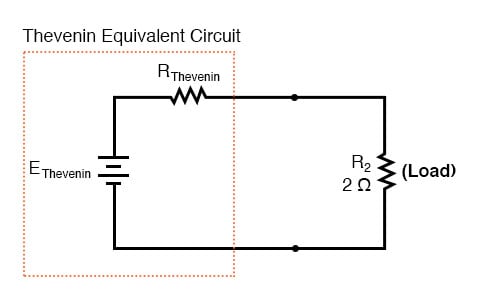
“Thevenin Equivalent Circuit” er den elektriske ækvivalent til B1, R1, R3 og B2 set fra de to punkter, hvor vores belastningsmodstand (R2) forbinder.
Thevenin-ækvivalent kredsløb, hvis den er korrekt afledt, vil opføre sig nøjagtigt det samme som det originale kredsløb dannet af B1, R1, R3 og B2. Med andre ord skal belastningsmodstanden (R2) spænding og strøm være nøjagtig den samme for den samme værdi af belastningsmodstand i de to kredsløb. Belastningsmodstanden R2 kan ikke “fortælle forskellen” mellem det oprindelige netværk af B1, R1, R3 og B2 og Thevenin-ækvivalent kredsløb for EThevenin og RThevenin, forudsat at værdierne for EThevenin og RThevenin er beregnet korrekt.
Fordelen ved at udføre “Thevenin-konvertering” til det enklere kredsløb er selvfølgelig, at det gør belastningsspænding og belastningsstrøm så meget lettere at løse end i det oprindelige netværk. Beregning af den ækvivalente Thevenin-kildespænding og seriemodstand er faktisk ret let. Først fjernes den valgte belastningsmodstand fra det originale kredsløb, erstattet med et brud (åbent kredsløb):

Bestem Thevenin Spænding
Dernæst bestemmes spændingen mellem de to punkter, hvor belastningsmodstanden, der tidligere var fastgjort, bestemmes. Brug de analysemetoder, der er til din rådighed, for at gøre dette. I dette tilfælde er det originale kredsløb med belastningsmodstanden fjernet intet andet end et simpelt seriekredsløb med modsatte batterier, og så kan vi bestemme spændingen over de åbne belastningsterminaler ved at anvende reglerne for seriekredsløb, Ohms lov og Kirchhoffs spænding Lov:

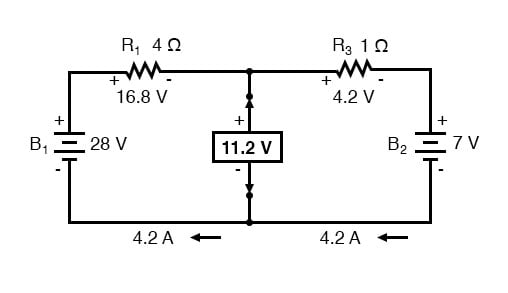
Spændingen mellem de to belastningsforbindelsespunkter kan regnes ud fra en af batteriets spændinger, og den ene af modstandens spænding falder og når ud til 11,2 volt.Dette er vores “Thevenin spænding” (EThevenin) i det tilsvarende kredsløb:

Bestem Thevenin Series Resistance
For at finde modstanden fra Thevenin-serien til vores ækvivalente kredsløb skal vi tage det originale kredsløb (med belastningsmodstanden stadig fjernet), fjerne strømkilderne (i samme stil som vi gjorde med Superpositionssætningen: spændingskilder erstattet med ledninger og aktuelle kilder erstattet med brud), og figur modstanden fra den ene belastningsterminal til den anden:

Med fjernelsen af de to batterier er den samlede modstand målt på dette sted lig med R1 og R3 parallelt: 0,8 Ω. Dette er vores “Thevenin-modstand” (RThevenin) for det ækvivalente kredsløb:

Bestem spændingen over belastningsmodstanden
Med belastningsmodstanden (2 Ω) fastgjort mellem forbindelsespunkterne kan vi bestemme spændingen over den og strøm igennem det som om hele netværket ikke var andet end et simpelt seriekredsløb:

Bemærk, at spænding og strøm tal for R2 (8 volt, 4 ampere) er identiske med dem, der findes ved hjælp af andre analysemetoder. Bemærk også, at spændings- og strømtallene for Thevenin-seriens modstand og Thevenin-kilden (total) ikke gælder for nogen komponent i det originale, komplekse kredsløb. Thevenins sætning er kun nyttig til at bestemme, hvad der sker med en enkelt modstand i et netværk: belastningen.
Fordelen er selvfølgelig, at du hurtigt kan bestemme, hvad der ville ske med den enkelte modstand, hvis den var af en anden værdi end 2 Ω uden at skulle gennemgå en masse analyse igen. Tilslut bare den anden værdi for belastningsmodstanden til Thevenin-ækvivalent kredsløb, og en lille smule seriekredsløbsberegning giver dig resultatet.
REVIEW:
- Thevenins sætning er en måde at reducere et netværk til et ækvivalent kredsløb sammensat af en enkelt spændingskilde, seriemodstand og seriebelastning.
- Trin, der skal følges for Thevenins sætning:
- Find Thevenin-kildespændingen ved at fjerne belastningsmodstanden fra det originale kredsløb og beregne spændingen over de åbne forbindelsespunkter, hvor belastningsmodstanden plejede at være.
- Find Thevenin-modstanden ved at fjerne alle strømkilder i det originale kredsløb (spændingskilder kortsluttet og aktuelle kilder åbne) og beregning af total modstand mellem de åbne forbindelsespunkter.
- Tegn Thevenin-ækvivalent kredsløb med Thevenins spændingskilde i serie med Thevenin-modstanden. Belastningsmodstanden fastgøres igen mellem de to åbne punkter i det tilsvarende kredsløb.
- Analyser spænding og strøm for belastningsmodstanden i henhold til reglerne for seriekredsløb.
RELATERET WORKSHEET:
- Thevenins, Nortons og Maximum Power Transfer Theorems Worksheet