A sum er resultatet af en tilføjelse. For eksempel tilføjer tilføjelse 1, 2, 3 og 4 summen 10, skrevet
 |
(1)
|
De numre, der summeres, kaldes tilføjelser eller undertiden summands. Summationsoperationen kan også angives ved hjælp af en stor sigma med øvre og nedre grænser skrevet over og under og indekset angivet nedenfor. F.eks. Kunne ovenstående sum skrives
 |
(2)
|
The summen af en liste med tal implementeres som Total.
En sum
 |
(3)
|
hvor hvert udtryk 
er givet af en eller anden fast regel (dvs. 
er en brønd -defineret sekvens) kaldes en (endelig) serie, og hvis antallet af udtryk 
er uendeligt, kaldes summen en uendelig serie (eller ofte bare en “serie”). En sum af formularen
 |
(4)
|
kaldes en geometrisk serie .
Betingelser for konvergens af en serie kan bestemmes i Wolfram-sproget ved hjælp af SumConvergence.
Den generelle endelige effektsum
 |
(5)
|
kan gives ved udtrykket
 |
(6)
|
hvilket svarer til Faulhabers formel, hvor notationen 
betyder mængden i spørgsmålet hæves til den passende magt 
, og alle vilkår for formen 
erstattes med det tilsvarende Bernoulli tal 
.
En morsom identitet på grund af J. Ziegenbein (pers. comm., 19. juni 2002) følger af identiteten
 |
(7)
|
som kan skrives
 |
(8)
|
Derfor 
kan for eksempel skrives i de tilsvarende former
 |
 |
 |
(9)
|
 |
 |
 |
(10)
|
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
og så videre.
Nicomachus sætning giver som nysgerrig udtryk for magtsummen 
.
Særlige summer inkluderer
 |
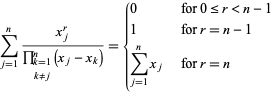(13)
|
og
 |
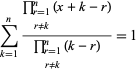(14)
|
For at minimere summen af et sæt firkanter af numre 
om et givet nummer 
 |
 |
 |
(15 )
|
 |
 |
 |
(16)
|
tag afledningen.
 |
(17)
|
Løsning for 
giver
 |
(18)
|
så 
minimeres, når 
er indstillet til betyder.