Lad os analysere et simpelt seriekredsløb og bestemme spændingsfaldet over individuelle modstande:
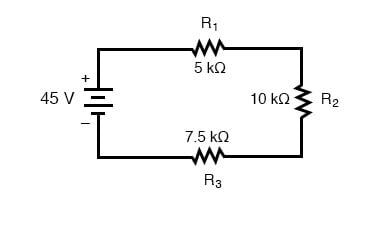

Fra de givne værdier for individuelle modstande kan vi bestemme en total kredsløbsmodstand, vel vidende at modstande tilføjes i serie:
Bestem den samlede kredsløbsmodstand

Herfra kan vi bruge Ohms lov (I = E / R) for at bestemme den samlede strøm, som vi ved vil være den samme som hver modstandsstrøm, idet strømme er ens i alle dele af et seriekredsløb:

Brug Ohms lov til at beregne strøm
Nu ved vi at vide, at kredsløbsstrømmen er 2 mA, kan vi bruge Ohms lov (E = IR) til at beregne spændingen over hver modstand:

Det skal være tydeligt, at spændingsfaldet over hver modstand er proportional med dens modstand, da strømmen er den samme gennem alle modstande. Læg mærke til, hvordan spændingen over R2 er dobbelt så stor som spændingen over R1, ligesom modstanden for R2 er dobbelt så stor som R1.
Hvis vi skulle ændre den samlede spænding, ville vi finde denne proportionalitet af spændingen dråber forbliver konstant:

Løsning af spændingsfaldsforhold
Spændingen over R2 er stadig nøjagtigt to gange det for R1s fald, på trods af at kildespændingen er ændret. Proportionaliteten af spændingsfald (forholdet mellem den ene og den anden) er strengt taget en funktion af modstandsværdier.
Med lidt mere observation bliver det tydeligt, at spændingsfaldet over hver modstand også er en fast andel af forsyningsspænding. Spændingen over R1 var for eksempel 10 volt, når batteriforsyningen var 45 volt. Da batterispændingen blev øget til 180 volt (4 gange så meget), steg spændingsfaldet over R1 også med en faktor 4 (fra 10 til 40 volt). Forholdet mellem R1s spændingsfald og total spænding ændrede sig dog ikke:

Ligeledes ingen af de andre spændingsfaldsforhold ændret med den øgede forsyningsspænding enten:

Spændingsdelerformel
Af denne grund , kaldes et seriekredsløb ofte en spændingsdeler for dets evne til at proportionere – eller dele – den samlede spænding i brøkdele med konstant forhold. Med en lille smule algebra kan vi udlede en formel til bestemmelse af seriemodstandsspændingsfald givet intet mere end total spænding, individuel modstand og total modstand:

Forholdet mellem individuel modstand og total modstand er det samme som forholdet mellem individuelt spændingsfald og den samlede forsyningsspænding i et spændingsdelerkredsløb. Dette er kendt som formlen for spændingsdeler, og det er en genvejsmetode til bestemmelse af spændingsfald i et seriekredsløb uden at gå igennem de aktuelle beregninger af Ohms lov.
Eksempel på brug af spændingsdelerformel
Ved hjælp af denne formel kan vi genanalyse eksemplets kredsløbsspændingsfald i færre trin:


Spænding – delende komponenter
Spændingsdelere finder bred anvendelse i elektriske målerkredsløb, hvor specifikke kombinationer af seriemodstande bruges til at “opdele ”En spænding i nøjagtige proportioner som en del af en spændingsmåleenhed.

Potentiometre som spændingsdelende komponenter
En enhed, der ofte bruges som en spændingsdelende komponent, er potentiometeret, som er en modstand med et bevægeligt element placeret ved en manuel drejeknap eller et håndtag. Det bevægelige element, typisk kaldet en visker, kommer i kontakt med en modstandsstreng ip af materiale (kaldes almindeligvis glidetråden, hvis den er lavet af resistiv metaltråd) på et hvilket som helst punkt valgt af den manuelle kontrol:

Viskerkontakten er det pil, der vender mod venstre, tegnet i midten af det lodrette modstandselement. Når den bevæges op, kontakter den modstandsstrimlen tættere på terminal 1 og længere væk fra terminal 2, sænker modstanden til terminal 1 og hæver modstanden til terminal 2. Når den bevæges ned, resulterer den modsatte effekt. Modstanden målt mellem klemme 1 og 2 er konstant for enhver viskerposition.
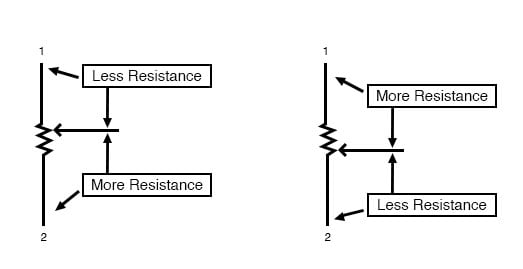
Roterende vs. lineære potentiometre
Her vises interne illustrationer af to potentiometertyper, roterende og lineære.
Lineære potentiometre

Nogle lineære potentiometre aktiveres ved en lineær bevægelse af en håndtag eller glideknap. Andre, som den, der er afbildet i den foregående illustration, aktiveres af en drejeskrue for finjusteringsevne.Sidstnævnte enheder kaldes undertiden trimpots, fordi de fungerer godt til applikationer, der kræver, at en variabel modstand “trimmes” til en eller anden præcis værdi.
Det skal bemærkes, at ikke alle lineære potentiometre har de samme terminalopgaver. som vist i denne illustration. Hos nogle er viskerterminalen i midten mellem de to endeterminaler.
Roterende potentiometer
Billedet nedenfor viser kropskonstruktionen af et roterende potentiometer .

Følgende fotografi viser et ægte, roterende potentiometer med synlig visker og glidetråd til nem visning. Akslen, der bevæger visker er blevet drejet næsten helt med uret, så viskeren næsten rører ved den venstre terminalende af glidetråden:

Her er det samme potentiometer med viskerakslen bevæget sig næsten helt mod urets position, så viskeren er nær den anden yderste ende af kørslen:

Effekter af justeringer i et potentiometer i et kredsløb
Hvis der påføres en konstant spænding mellem de ydre terminaler (på tværs af glidetråden) , aftørrer viskerpositionen en brøkdel af den påførte spænding, der kan måles mellem viskerens kontakt og en af de to andre terminaler. Brøkværdien afhænger helt af viskerens fysiske position:
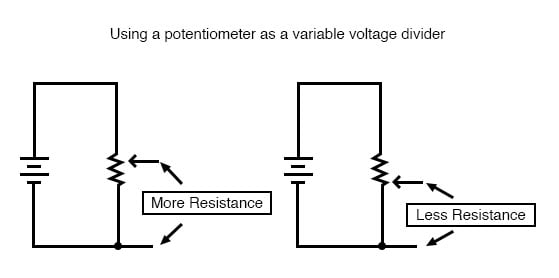
Betydningen af potentiometerapplikation
Ligesom den faste spændingsdeler er potentiometerets spændingsdelingsforhold strengt taget en funktion af modstand og ikke af størrelsen af den anvendte spænding. Med andre ord, hvis potentiometerknappen eller håndtaget flyttes til positionen 50 procent (nøjagtig center), ville spændingen, der faldt mellem viskeren og den ene eller den anden terminal, være nøjagtigt 1/2 af den anvendte spænding, uanset hvilken spænding der sker være, eller hvad potentiometerets ende-til-ende-modstand er. Med andre ord fungerer et potentiometer som en variabel spændingsdeler, hvor spændingsdelingsforholdet er indstillet af viskerposition.
Denne anvendelse af potentiometeret er et meget nyttigt middel til at opnå en variabel spænding fra en fast spænding kilde, f.eks. et batteri. Hvis et kredsløb, du bygger, kræver en vis spænding, der er mindre end værdien af et tilgængeligt batterispænding, kan du forbinde de ydre terminaler på et potentiometer på tværs af dette batteri og “ringe op”, uanset hvilken spænding du har brug for, mellem potentiometeret visker og en af de ydre terminaler til brug i dit kredsløb:

Når det bruges på denne måde, gør navnet potentiometer perfekt følelse: de måler (styrer) potentialet (spænding), der anvendes over dem ved at skabe et variabelt spændingsdelingsforhold. Denne anvendelse af det tre-terminale potentiometer som en variabel spændingsdeler er meget populær i kredsløbsdesign.
Prøver af små potentiometre
Her vises flere små potentiometre af den art, der almindeligvis anvendes i forbrugerelektronisk udstyr og af hobbyister og studerende i konstruktion af kredsløb:

De mindre enheder meget til venstre og meget højre er designet til at tilslutte en lodde s brødbræt eller loddes på et printkort. Midtenhederne er designet til at blive monteret på et fladt panel med ledninger loddet til hver af de tre terminaler. Her er tre flere potentiometre, mere specialiserede end det netop viste sæt:

Den store “Helipot” -enhed er et laboratoriepotentiometer designet til hurtig og nem tilslutning til et kredsløb. Enheden i nederste venstre hjørne af fotografiet er den samme type potentiometer, bare uden et kabinet eller 10-omdrejningstæller. Begge disse potentiometre er præcisionsenheder, der bruger multi- drej modstandsstrimler til spiralformede spor og viskermekanismer til at foretage små justeringer. Enheden nederst til højre er et panelmonteret potentiometer designet til grov service i industrielle applikationer.
ANMELDELSE:
- Seriekredsløb andel, eller divider, den samlede forsyningsspænding blandt individuelle spændingsfald, proportionerne er strengt afhængige af modstande: ERn = ETotal (Rn / RTotal)
- Et potentiometer er en variabel- modstandskomponent med tre forbindelsespunkter, ofte brugt som en justerbar spændingsdeler.
RELATERET WO RKSHEETS:
- Arbejdsark for spændingsdelerkredsløb