Introduktion til k-nærmeste naboer: En stærk maskinlæringsalgoritme (med implementering i Python & R)

Bemærk: Denne artikel blev oprindeligt offentliggjort den 10. oktober 2014 og opdateret den 27. marts 2018

Oversigt

• Forstå k nærmeste nabo (KNN) – en af de mest populære maskinindlæringsalgoritmer
• Lær hvordan kNN fungerer i python
• Vælg den rigtige værdi af k i enkle vendinger

Introduktion

I de fire år af min datavidenskabelige karriere har jeg bygget mere end 80% klassificeringsmodeller og kun 15-20% regressionsmodeller. Disse forhold kan mere eller mindre generaliseres i hele branchen. Årsagen til denne bias mod klassificeringsmodeller er, at de fleste analytiske problemer involverer at tage en beslutning.

Vil en kunde f.eks. Attrere eller ikke, hvis vi målretter mod kunde X for digitale kampagner, hvad enten kunden har et stort potentiale osv. Disse analyser er mere indsigtsfulde og direkte knyttet til en implementeringskøreplan.

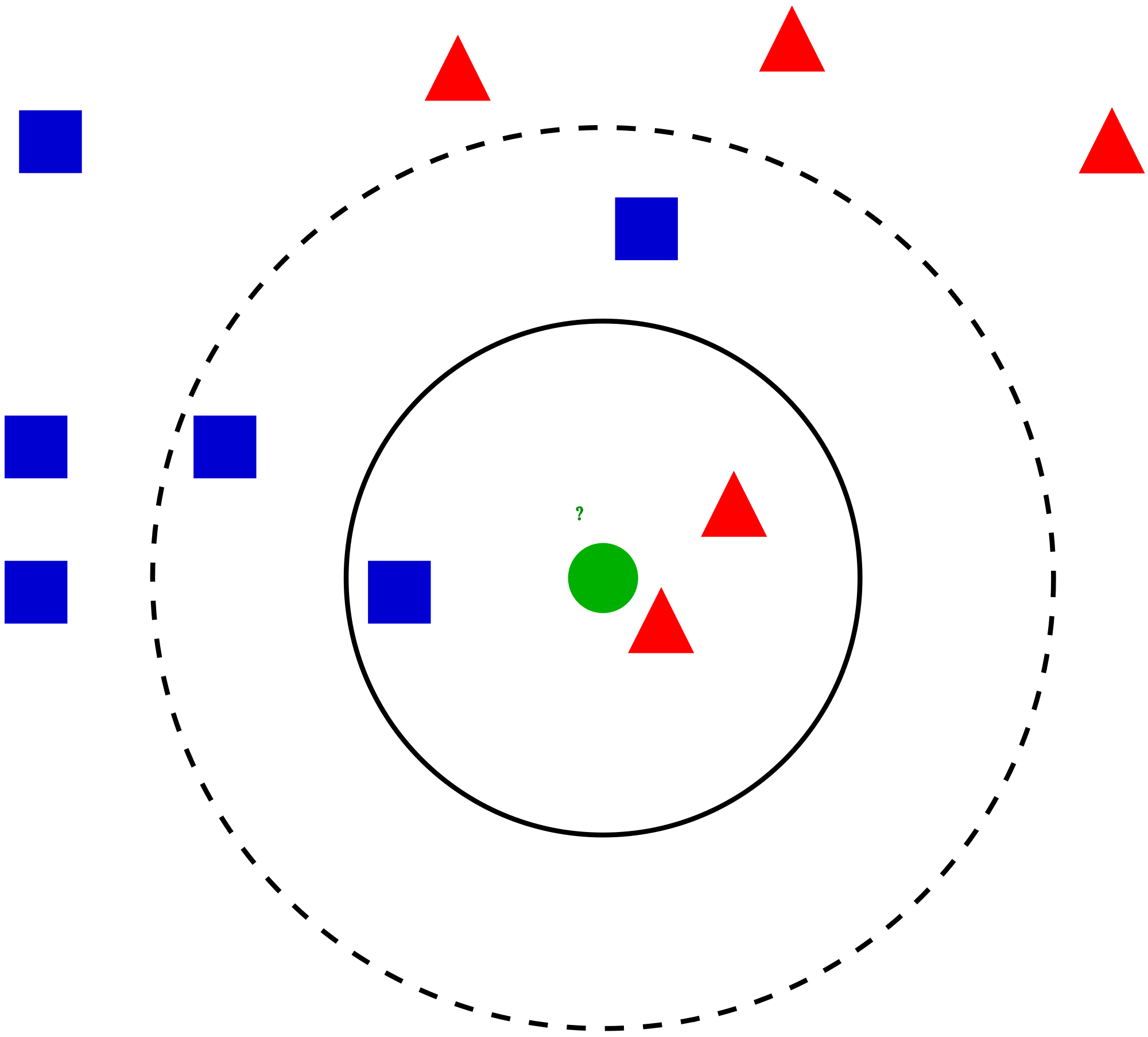
I denne artikel vil vi tale om en anden meget anvendt klassificeringsteknik for maskinindlæring kaldet K-nærmeste naboer (KNN). Vores fokus vil primært være på, hvordan algoritmen fungerer, og hvordan påvirker inputparameteren output / forudsigelse.

Bemærk: Folk, der foretrækker at lære gennem videoer, kan lære det samme gennem vores gratis kursus – K- Nærmeste naboer (KNN) -algoritme i Python og R. Og hvis du er en komplet nybegynder til datalogi og maskinindlæring, så tjek vores Certified BlackBelt-program –

• Certificeret AI & ML Blackbelt + -program

Indholdsfortegnelse

• Hvornår bruger vi KNN-algoritme?
• Hvordan fungerer KNN-algoritme fungerer?
• Hvordan vælger vi faktoren K?
• Breaking it Down – Pseudo Code of KNN
• Implementering i Python fra bunden
• Sammenligning af vores model med scikit-læring

Hvornår bruger vi KNN-algoritme?

KNN kan bruges til begge forudsigelige problemer med klassificering og regression. Det bruges dog mere i klassificeringsproblemer i branchen. For at evaluere enhver teknik ser vi generelt på 3 vigtige aspekter:

1. Nem at fortolke output

2. Beregningstid

3. Forudsigelig kraft

Lad os tage et par eksempler for at placere KNN i skalaen:

KNN algoritme messer på tværs af alle parametre af overvejelser. Det bruges almindeligvis på grund af dets lette fortolkning og lave beregningstid.

Hvordan fungerer KNN-algoritmen?

Lad os tage en simpel sag til forstå denne algoritme. Følgende er en spredning af røde cirkler (RC) og grønne firkanter (GS):

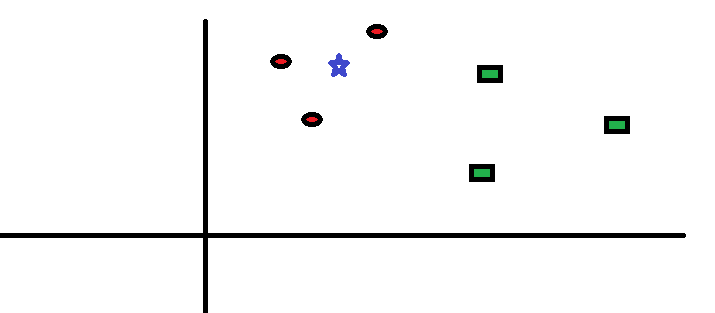Du har til hensigt at finde ud af klassen af den blå stjerne (BS). BS kan enten være RC eller GS og intet andet. “K” er KNN-algoritmen er den nærmeste nabo, vi ønsker at tage afstemningen fra. Lad os sige K = 3. Derfor laver vi nu en cirkel med BS som centrum lige så stort som kun at vedlægge tre datapunkter på flyet Se følgende diagram for flere detaljer:

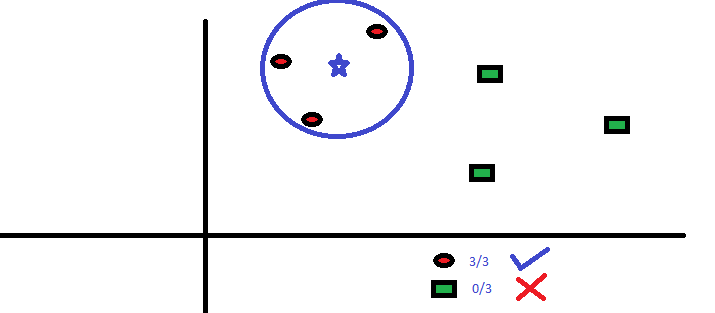De tre nærmeste punkter til BS er alle RC. med et godt tillidsniveau kan vi sige, at BS skulle tilhøre klassen RC. Her blev valget meget indlysende, da alle tre stemmer fra den nærmeste nabo gik til RC. Valget af parameter K er meget afgørende i denne algoritme Dernæst vil vi forstå, hvilke faktorer der skal betragtes som den bedste K.

Hvordan vælger vi faktoren K?

Lad os først forstå, hvad præcist påvirker K i algoritmen. Hvis vi ser det sidste eksempel, da alle de 6 træningsobservation forbliver konstante, kan vi med en given K-værdi skabe grænser for hver klasse. se grænser adskiller RC fra GS. Lad os på samme måde se effekten af værdi “K” på klassegrænserne. Følgende er de forskellige grænser, der adskiller de to klasser med forskellige værdier af K.

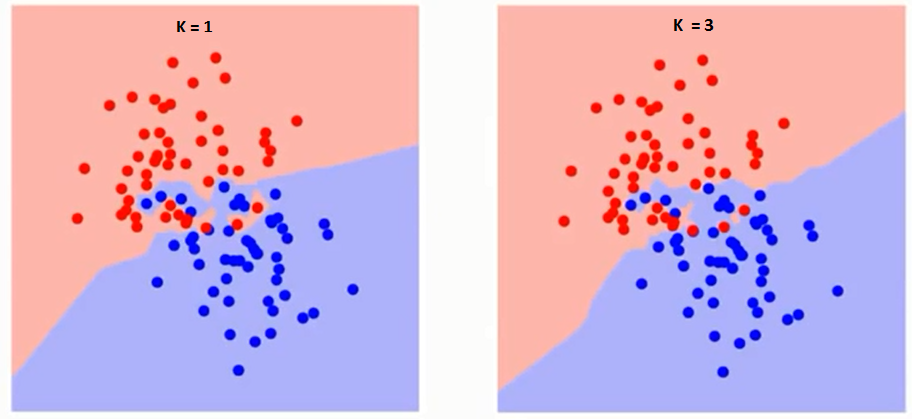
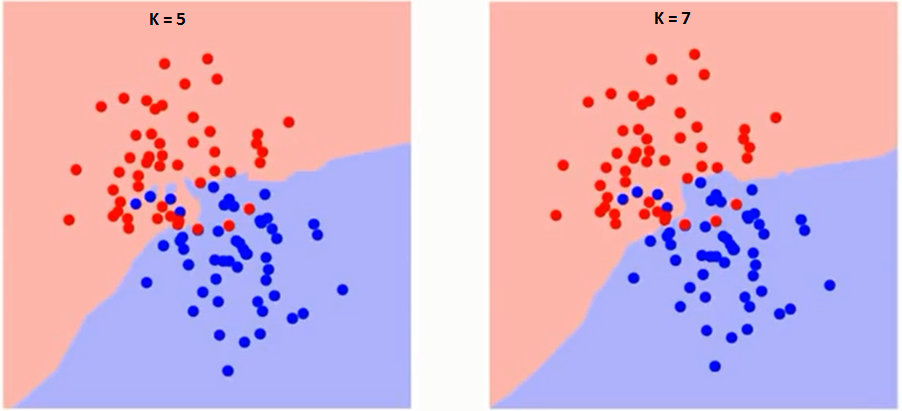
Hvis du ser nøje, kan du se det grænsen bliver glattere med stigende værdi af K. Med K stigende til uendelig bliver den endelig helt blå eller helt rød afhængigt af det samlede flertal. Træningsfejlfrekvensen og valideringsfejlfrekvensen er to parametre, som vi har brug for for at få adgang til forskellige K-værdier. Følgende er kurven for træningsfejlfrekvensen med en varierende værdi på K:

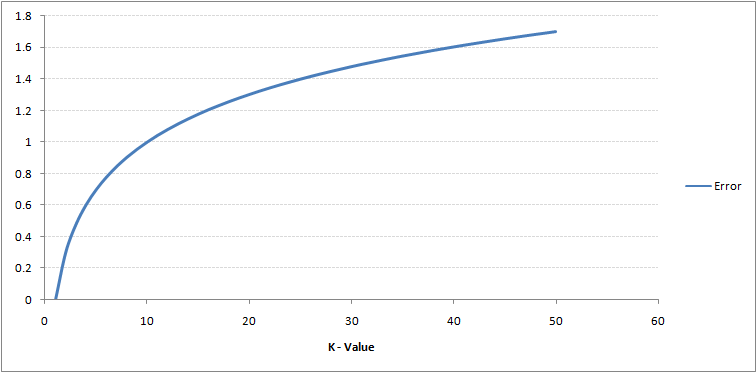Som du kan se, fejlprocent ved K = 1 er altid nul for træningsprøven.Dette skyldes, at det nærmeste punkt til et træningsdatapunkt er selve, og forudsigelsen er derfor altid nøjagtig med K = 1. Hvis valideringsfejlkurve ville have været ens, ville vores valg af K have været 1. Følgende er valideringsfejlkurve med varierende værdi på K:

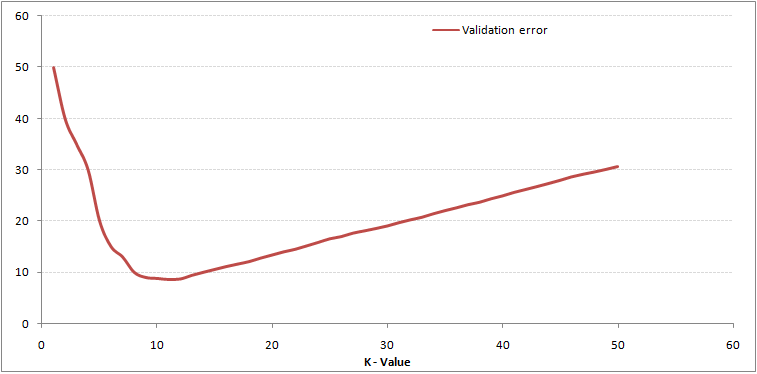Dette gør historien mere klar. Ved K = 1 overmonterede vi grænserne. Derfor falder fejlhastigheden oprindeligt og når et minimum. Efter minima-punktet øges det med stigende K. For at få den optimale værdi af K kan du adskille træning og validering fra det oprindelige datasæt. Plot nu valideringsfejlkurven for at få den optimale værdi af K. Denne værdi af K skal bruges til alle forudsigelser.

Ovenstående indhold kan forstås mere intuitivt ved hjælp af vores gratis kursus – K-nærmeste naboer ( KNN) Algoritme i Python og R

Breaking it Down – Pseudo Code of KNN

Vi kan implementere en KNN-model ved at følge nedenstående trin:

1. Indlæs dataene
2. Initialiser værdien af k
3. For at få den forudsagte klasse skal du gentage fra 1 til det samlede antal træningsdatapunkter
   1. Beregn afstanden mellem test data og hver række træningsdata. Her bruger vi euklidisk afstand som vores afstandsmetrik, da det er den mest populære metode. De andre målinger, der kan bruges, er Chebyshev, cosinus osv.
   2. Sorter de beregnede afstande i stigende rækkefølge baseret på afstandsværdier
   3. Få de øverste k-rækker fra det sorterede array
   4. Få den hyppigste klasse af disse rækker
   5. Returner den forudsagte klasse

Implementering i Python fra bunden

Vi bruger det populære Iris-datasæt til at opbygge vores KNN-model. Du kan downloade den herfra.

Sammenligning af vores model med scikit-læring

Vi kan se, at begge modeller forudsagde den samme klasse (Iris- virginica ) og de samme nærmeste naboer (). Derfor kan vi konkludere, at vores model kører som forventet.

Implementering af kNN i R

Trin 1: Import af data

Trin 2: Kontrol af data og beregning af dataoversigten

Output

Trin 3: Opdeling af data

Trin 4: Beregning den euklidiske afstand

Trin 5: Skrivning af funktionen til forudsigelse af kNN

Trin 6: Beregning af etiketten (navn) for K = 1

Output

For K=1 "Iris-virginica"

På samme måde kan du beregne for andre værdier af K.

Sammenligning af vores kNN-forudsigelsesfunktion med “Class” -biblioteket

Output

For K=1 "Iris-virginica"

Vi kan se, at begge modeller forudsagde den samme klasse (Iris-virginica).

Slutnoter

KNN-algoritme er en af de enkleste klassificeringsalgoritmer. Selv med sådan enkelhed kan det give meget konkurrencedygtige resultater. KNN-algoritme kan også bruges til regressionsproblemer. Den eneste forskel fra den diskuterede metode vil man bruge gennemsnit af nærmeste naboer i stedet for at stemme fra nærmeste naboer. KNN kan kodes i en enkelt linje på R. Jeg skal endnu undersøge, hvordan vi kan bruge KNN-algoritme på SAS.

Fandt du artiklen nyttig? Har du brugt noget andet maskinindlæringsværktøj for nylig? Planlægger du at bruge KNN i nogle af dine forretningsproblemer? Hvis ja, del med os, hvordan du planlægger at gøre det.

Hvis du kan lide det, du lige har læst & vil du fortsætte din analytiske læring, så abonner på vores e-mails, følg os på twitter eller synes godt om vores facebook-side.