Hvad er BFS-algoritme (Breadth-First Search)?
Breadth-first search (BFS) er en algoritme, der bruges til at tegne data eller søge i træ- eller traverseringsstrukturer. Den fulde form for BFS er den første søgning i bredde.
Algoritmen besøger og markerer effektivt alle nøgleknuderne i en graf nøjagtigt i bredden. Denne algoritme vælger en enkelt knude (start- eller kildepunkt) i en graf og besøger derefter alle knudepunkter, der støder op til den valgte knude. Husk, BFS får adgang til disse noder en efter en.
Når algoritmen besøger og markerer startknudepunktet, bevæger den sig mod de nærmeste ubesøgte noder og analyserer dem. Når de er besøgt, markeres alle noder. Disse gentagelser fortsætter, indtil alle knudepunkterne i grafen er blevet besøgt og markeret.
I denne algoritmevejledning lærer du:
- Hvad er BFS-algoritme (bredde-første søgning)?
- Hvad er grafgennemgange?
- Arkitekturen for BFS-algoritme
- Hvorfor har vi brug for BFS-algoritme?
- Hvordan fungerer BFS-algoritme?
- Eksempel på BFS-algoritme
- Regler for BFS-algoritme
- Anvendelser af BFS-algoritme
Hvad er grafgennemgange?
En grafgennemgang er en almindeligt anvendt metode til at lokalisere toppunktpositionen i grafen. Det er en avanceret søgealgoritme, der kan analysere grafen med hastighed og præcision sammen med markering af rækkefølgen af de besøgte hjørner. Denne proces giver dig mulighed for hurtigt at besøge hver node i en graf uden at være låst i en uendelig løkke.
Arkitekturen for BFS-algoritme
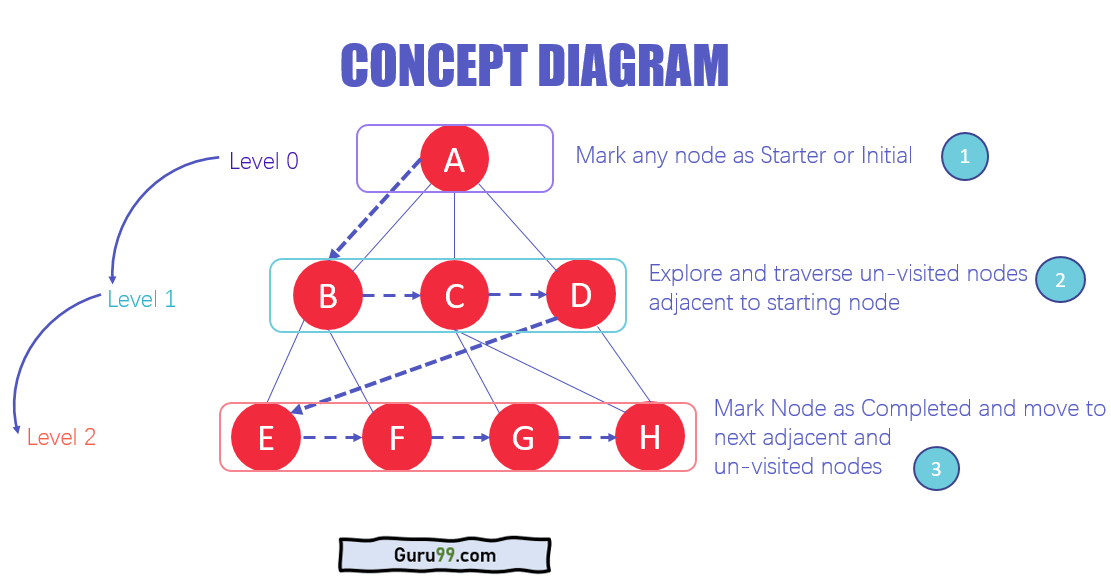
- I de forskellige niveauer af data kan du markere enhver node som start eller startknude for at begynde at krydse. BFS besøger noden og markerer den som besøgt og placerer den i køen.
- Nu besøger BFS de nærmeste og ikke-besøgte noder og markerer dem. Disse værdier føjes også til køen. Køen fungerer på FIFO-modellen.
- På lignende måde analyseres de resterende nærmeste og ubesøgte noder på grafen markeret og føjes til køen. Disse emner slettes fra køen som modtagelse og udskrives som resultat.
Hvorfor har vi brug for BFS-algoritme?
Der er adskillige grunde til at bruge BFS-algoritmen til at bruge som søgning efter dit datasæt. Nogle af de mest vitale aspekter, der gør denne algoritme til dit første valg, er:
- BFS er nyttig til at analysere noderne i en graf og konstruere den korteste vej til at krydse gennem disse.
- BFS kan krydse gennem en graf i det mindste antal iterationer.
- BFS-algoritmens arkitektur er enkel og robust.
- Resultatet af BFS-algoritmen har en høj grad af nøjagtighed sammenlignet med andre algoritmer.
- BFS-iterationer er sømløse, og der er ingen mulighed for, at denne algoritme bliver fanget i et uendeligt løkkeproblem.
Hvordan fungerer BFS-algoritme?
Grafgennemgang kræver, at algoritmen besøger, kontrollerer og / eller opdaterer hver eneste ikke-besøgte node i en trælignende struktur. Grafgennemgang er kategoriseret efter rækkefølgen, i hvilken de besøger noderne på grafen.
BFS-algoritme starter operationen fra den første eller startknudepunkt i en graf og krydser den grundigt. Når den med succes krydser den oprindelige knude, besøges og markeres det næste ikke-krydsede toppunkt i grafen.
Derfor kan du sige, at alle knudepunkter, der støder op til det aktuelle toppunkt, bliver besøgt og krydset i den første iteration. En simpel kømetode bruges til at implementere funktionen af en BFS-algoritme, og den består af følgende trin:
Trin 1)

Hvert toppunkt eller knudepunkt i grafen er kendt. For eksempel kan du markere noden som V.
Trin 2)

Hvis toppunktet V ikke er tilgængeligt, skal du tilføje toppunktet V i BFS-køen
Trin 3)

Start BFS-søgningen, og efter afslutning markerer du topstykke V som besøgt.
Trin 4)

BFS-køen er stadig ikke tomt, fjern derfor toppunktet V på grafen fra køen.
Trin 5)

Hent alle de resterende hjørner på grafen, der støder op til toppunktet V
Trin 6)

Lad os sige V1 for hvert tilstødende toppunkt, hvis det ikke er besøgt endnu, skal du tilføje V1 til BFS-køen
Trin 7)

BFS besøger V1 og markerer det som besøgt og sletter det fra køen.
Eksempel BFS-algoritme
Trin 1)

Du har en graf over syv tal fra 0 til 6.
Trin 2)

0 eller nul er markeret som en rodknude.
Trin 3)

0 besøges, markeres og indsættes i kødatastrukturen.
Trin 4)
Resterende 0 tilstødende og ikke-besøgte noder besøges, markeres og indsættes i køen.
Trin 5)

Kørselsgentagelser gentages, indtil alle noder er besøgt.
Regler for BFS-algoritme
Her er vigtige regler for brug af BFS-algoritme:
- En kø (FIFO-First in First Out) datastruktur bruges af BFS.
- Du markerer en hvilken som helst node i grafen som rod og begynder at krydse dataene fra den.
- BFS krydser alle knudepunkterne i grafen og slipper dem fortsat som færdige.
- BFS besøger en tilstødende ubesøgt node, markerer den som færdig og indsætter den i en kø.
- Fjerner det forrige toppunkt fra køen, hvis der ikke findes nogen tilstødende toppunkt.
- BFS-algoritme gentager, indtil alle hjørnerne i grafen er gennemgået og markeret som afsluttet.
- Der er ingen sløjfer forårsaget af BFS under gennemkørsel af data fra nogen node.
Anvendelser af BFS-algoritme
Lad os tage en se på nogle af de virkelige applikationer, hvor en BFS-algoritmeimplementering kan være yderst effektiv.
- Uvægtede grafer: BFS-algoritme kan nemt skabe den korteste sti og et minimum spændende træ for at besøge alle hjørnerne i grafen på kortest mulig tid med høj nøjagtighed.
- P2P-netværk: BFS kan implementeres for at lokalisere alle de nærmeste eller nærliggende noder i et peer-to-peer-netværk. Dette vil finde de krævede data hurtigere .
- Webcrawlere: Søgemaskiner eller webcrawlere kan nemt opbygge flere niveauer af indekser ved at anvende BFS. BFS-implementering starter fra kilden, som er websiden, og besøger derefter alle links fra den kilde .
- Navigationssystemer: BFS kan hjælpe med at finde alle de omkringliggende placeringer fra hoved- eller kildeplaceringen.
- Netværkssendelse ing: En udsendt pakke styres af BFS-algoritmen til at finde og nå alle de noder, den har adressen til.
Oversigt
- En grafgennemgang er en unik proces, der kræver, at algoritmen besøger, kontrollerer og / eller opdaterer hver eneste ikke-besøgte node i en trælignende struktur. BFS algoritme fungerer på et lignende princip.
- Algoritmen er nyttig til at analysere knudepunkterne i en graf og konstruere den korteste vej til at krydse gennem disse.
- Algoritmen krydser grafen i det mindste antal iterationer og den kortest mulige tid.
- BFS vælger en enkelt knude (start- eller kildepunkt) i en graf og besøger derefter alle knudepunkter, der støder op til den valgte knude. BFS får adgang til disse noder en efter en.
- De besøgte og markerede data placeres i en kø af BFS. En kø fungerer på en først ind-ud-basis. Derfor slettes det element, der er placeret i grafen først, og udskrives som et resultat.
- BFS-algoritmen kan aldrig blive fanget i en uendelig løkke.
- På grund af høj præcision og robust implementering bruges BFS i flere virkelige løsninger som P2P-netværk, webcrawlere, og netværksudsendelse.