Hvordan varierer trykket med volumenændring under adiabatisk ekspansion og kompression i en ideel gas? Denne side er et bilag til vores diskussion af lyd. Luft ved atmosfærisk tryk er en næsten ideel gas, og lydtransmission i luft er tæt på adiabatisk for normale frekvenser og transmissionsafstande. (Vi vender tilbage til denne antagelse nedenfor.)
Den første lov om termodynamik relaterer ændringen i intern energi dU til arbejdet dW udført af et system og varmen dQ tilføjet til det.
dU = dQ – dW
I en adiabatisk proces er det varmeudvekslede dQ = definition 0. At erstatte dette i den første lov og omarrangere giver
0 = dQ = dU + dW
Det andet udtryk er let: arbejdet udført dW, når et system ændrer lydstyrken V med dV, er PdV.
Det første udtryk kan være relateret til den specifikke varme, der er defineret som den tilsatte varme pr. enhedstemperaturændring pr. mol stof. Hvis vi tilføjer varme ved konstant volumen, ekspanderer gassen ikke, og det fungerer heller ikke. Så den ekstra varme øger den interne energi U. Så det følger, at definitionen, at den specifikke varme ved konstant volumen er ![]() , hvor n er antallet af mol. Derfor
, hvor n er antallet af mol. Derfor
Nu er tilstandsligningen for en ideel gas
nRT = PV ( ii)
hvor R er gaskonstanten. At tage derivater giver
Vi kan nu kombinere ligninger (i) og (iii) for at eliminere T. (i) og (ii) giver henholdsvis disse udtryk for ncv dT:
Indsamling af PdV- og VdP-termerne giver
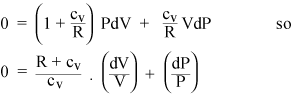
Hvis gassen nu er ideel, er dens indre energi al kinetisk, så den indre energi U afhænger kun af T. Fra tilstandsligningen for en ideel gas (ii) kan vi beregne arbejdet dW udført ved konstant tryk: det er bare PdV = nRdT. Så hvis vi tilføjer varme til en gas ved konstant tryk, er vi nødt til at opvarme ekstra RDT for hver mol gas ud over den varme, vi skal tilføje ved konstant volumen. Så den specifikke varme for en ideel gas ved konstant tryk er bare cP = cv + R. Forholdet mellem specifikke varmer gives et standardsymbol:
. Så vi har
(iv)
Dette er hovedresultatet, som vi har brug for for at diskutere lydbølger: vi har netop vist, at den proportionelle ændring i tryk er – γ gange den proportionelle ændring i volumen eller γ gange den proportionelle ændring i densitet. >
Lad os dog ikke stoppe her, fordi vi kun er et par linjer væk fra et vigtigt resultat. Vi ved, at d (ln x) = dx / x (se beregning for et bevis). Så vi kan skrive den foregående ligning som
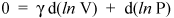
og omarrangere det for at give
(v)
Derfor til en adiabatisk proces i en ideel gas,
. (vi)
Ved refleksion er du enig i, at cP > cV: At konstant volumen, alt th Den varme, du lægger i, går til at øge den indre energi og dermed hæve temperaturen. Ved konstant tryk skal du ikke kun lægge den varme, der hæver den interne energi, men også en mængde varme svarende til det arbejde, der udføres, når systemet gennemgår termisk ekspansion. For luft er γ ca. 1,4.
Selvfølgelig kan vi nu erstatte i (vi) fra tilstandsligningen (ii) for at se, hvordan P og T eller T og V er relateret til en adiabatisk proces.
Hvornår er lyd adiabatisk?
Vi nævnte ovenfor, at “lydtransmission i luft er tæt på adiabatisk for normale frekvenser og transmissionsafstande”. Hvornår mislykkes dette? Ved trykmaxima i en lydbølge er temperaturen høj. Så vi forventer, at noget varme vil diffundere til de tilstødende trykminima. Selvfølgelig i en halv periode af en lydbølge er der ikke meget tid til varme til at diffundere en halv bølgelængde. Imidlertid går den tid, det tager for varmen at diffundere, som afstanden. Så denne proces er mindre ubetydelig for høje frekvenser, fordi den kortere halvbølgelængde mere end kompenserer for den kortere halvperiode. Denne diffusion tager mekanisk energi ud af bølgen, især ved høje frekvenser, og effekten stiger med transmissionsafstanden.Af denne grund (og nogle gange andre) er fjerne lyde ikke kun mindre høje, men også mindre lyse end tætte.