Når man udfører en restanalyse, er et “residuals versus fit-plot” det hyppigst oprettede plot. Det er et spredningsdiagram over rester på y-aksen og monterede værdier (estimerede svar) på x-aksen. Diagrammet bruges til at detektere ikke-linearitet, ulige fejlvariationer og outliers.
Lad os se på et eksempel for at se, hvordan et “velopdragen” restplot ser ud. Nogle forskere (Urbano- Marquez et al., 1989) var interesseret i at afgøre, om alkoholforbrug var lineært relateret til muskelstyrke. Forskerne målte det samlede levetidforbrug af alkohol (x) på en tilfældig prøve på n = 50 alkoholiske mænd. De målte også styrken (y) af deltamuskulaturen i hver persons ikke-dominerende arm. Et tilpasset linjediagram over de resulterende data (alcoholarm.txt) ser ud som:
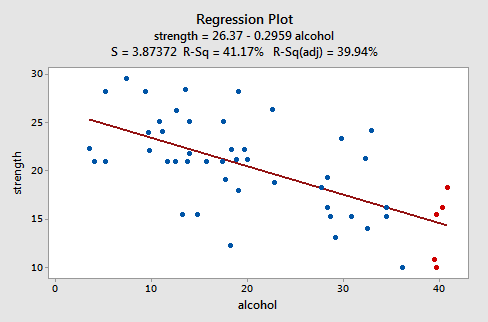
Handlingen antyder, at der er et faldende lineært forhold mellem alkohol og armstyrke. Det antyder også, at der ikke er usædvanlige datapunkter i datasættet. Og det illustrerer, at variationen omkring den anslåede regressionslinje er konstant, hvilket antyder, at antagelsen om lige fejlvariationer er rimelig.
Her ser de tilsvarende rester versus passer-plot ud for datasættet “s enkel lineær regressionsmodel med armstyrke som respons og niveau af alkoholforbrug som forudsigeren:
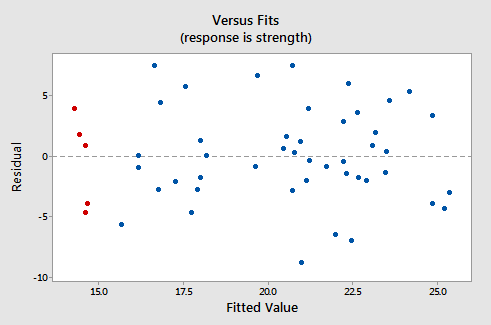
Bemærk, at som defineret, residualerne vises på y-aksen, og de monterede værdier vises på x-aksen. Du skal være i stand til at se tilbage på spredningsdiagrammet for dataene og se, hvordan datapunkterne der svarer til datapunkterne i det resterende versus passer-plot her. Hvis du har problemer med at gøre det, skal du kigge på de fem datapunkter i det originale spredningsdiagram, der vises i rødt. Bemærk, at disse mænds (hvis alkoholforbrug er omkring 40) er forudsagt svar (tilpasset værdi) er omkring 14 Bemærk også det mønster, hvor de fem datapunkter afviger fra den anslåede regressionslinje.
Se nu på, hvordan og hvor disse fem datapunkter vises i residual versus versus plot. Deres monterede værdi er ca. 14 og deres afvigelse fra den resterende linje = 0 deler det samme mønster som deres afvigelse fra den estimerede regressionslinje. Ser du forbindelsen? Ethvert datapunkt, der falder direkte på den estimerede regressionslinje, har en rest på 0. Derfor er den resterende = 0 linje svarer til den anslåede regressionslinje.
Dette plot er et klassisk eksempel på et velopdragen residual vs. passer-plot. Her er karakteristikaene for et velopdragen rest vs. passer-plot og hvad de foreslå, om det enkle er passende e lineær regressionsmodel:
- Resterne “spretter tilfældigt” omkring 0-linjen. Dette antyder, at antagelsen om, at forholdet er lineært, er rimelig.
- Resterne danner groft et “vandret bånd” omkring 0-linjen. Dette antyder, at afvigelserne i fejltermerne er ens.
- Ingen resterende “skiller sig ud” fra det grundlæggende tilfældige mønster af rester. Dette antyder, at der ikke er nogen outliers.
Generelt vil du have, at dine resterende vs. passer-plot skal se ud som det ovenstående plot. Glem ikke, at fortolkning af disse plot er subjektiv. Min erfaring har været, at studerende, der lærer restanalyse for første gang, har tendens til at fortolke disse plot, når de ser på hvert twist og turn som noget, der potentielt er besværligt. Du vil især gerne være forsigtig med at lægge for meget vægt på restkomponenter baseret på små datasæt. Undertiden er datasættene bare for små til at fortolke fortolkningen af en rest vs. Du skal ikke bekymre dig! Du lærer – med praksis – hvordan man “læser” disse plot.