Antag at luft pumpes ned i et glat rundt rør, som har en konstant diameter bortset fra et afsnit i midten, hvor røret indsnævres ned til halv diameter og udvider sig derefter igen. Antag, at alle ændringer i diameter finder sted jævnt, og luften strømmer støt ned ad røret uden hvirvler eller turbulens.
Træning
hvor i røret forventer du trykket for at være størst?
Svar
De fleste mennesker spurgte dette for første gang forudsiger, at trykket vil være størst i den smalle del af røret. Men faktisk, hvis vi rent faktisk udfører eksperimentet, ved at lægge manometre på forskellige punkter langs røret, finder vi modsat intuitivt, at lufttrykket er lavest, hvor luften bevæger sig hurtigst!

For at se hvordan dette kunne være, vil vi anvende de teknikker, vi udviklede for at finde ud af, hvordan trykket varierede i en stationær væske. Den måde, vi gjorde det på, var ved at tegne et frit kropsdiagram for en lille cylinder med væske. Da denne lille cylinder var i ro, var den samlede kraft på den nul, så nettotrykket afvejede vægten. Overvej nu en konstant bevægende væske. Det er nyttigt at visualisere strømmen ved at tegne strømlinjer, linjer, så deres retning er den retning, væsken bevæger sig i på hvert punkt.

Faktisk fortæller disse strømline dig ikke kun retningen, væsken bevæger sig i, men giver også en ide om hastigheden – hvor de kommer tættere på hinanden, skal væsken bevæge sig hurtigere, fordi den samme mængde væske strømmer gennem en smallere region. Forestil dig nu en luftcylinder, der bevæger sig langs røret, hvis akse er parallel med strømlinjen. Det skal selvfølgelig være hurtigere, når det kommer ind i den smalle del af røret – da den samme mængde luft strømmer gennem den smalle del som den brede del, skal den gå hurtigere.
Men hvis den lille væskecylinder accelererer, skal den påvirkes af en kraft, der skubber den bagfra.
Dens vægt er irrelevant her, da den bevæger sig vandret. Derfor er den eneste kraft, der virker på det, trykket, og vi må konkludere, at trykket bagpå er større end trykket på fronten. Derfor skal trykket falde, når det kommer ind i den smalle del. For at gøre det tydeligere, hvad der foregår, tegner vi en ret stor cylinder:
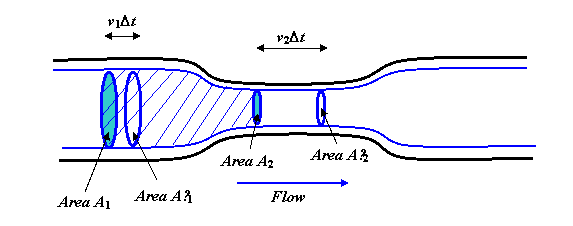
Væsken strømmer jævnt og jævnt langs røret. De tykke blå linjer er strømlinjeformede, faktisk skulle du forestille dig at dreje hele diagrammet omkring den centrale akse for at få et tredimensionelt billede, og de blå linjer ville blive en cylinder med et smallere “hals” -snit, der gentager formen på rør.
Overvej nu væskelegemet inden for de viste strømlinjer og er begrænset til de to ender af de cirkulære områder A1 og A2. Strømningshastigheden af væske over A1 skal være den samme som hastigheden af strømme over A2, fordi væske i jævn strøm ikke kan ophobes i midten (eller nedbrydes derfra heller). Volumenet, der strømmer over A1 på et sekund, er v1A1. (For at se dette, forestil dig et langt lige rør uden et smalt del. Hvis væsken flyder med, lad os sige 3 meter pr. sekund, så vil al væske, der var inden for 3 meter fra området A1 på opstrøms siden, i et sekund have strømmet igennem.)
Så, flow over A1 er lig med flow over A2, \
(fodnote: Det er måske værd at nævne, at vi implicit antager veloci ty er den samme på alle punkter i område A1. Enhver ægte væske har en vis viskositet (friktion) og vil bevæge sig langsommere nær siderne af røret end i midten. Vi diskuterer dette senere. For øjeblikket betragter vi en “ideel” væske, det udtryk, der bruges, når man ignorerer viskositet. Faktisk er det resultat, vi udleder, ok – vi kunne have taget et lille område A1 langt væk fra siderne, så hastigheden ville have været det samme for hele området, men det ville have givet et meget mindre klart diagram.)
Vi er nu klar til at undersøge forøgelsen i væskens kinetiske energi, når den kommer op i den smalle del, og forstå, hvordan trykforskellen udførte det arbejde, der var nødvendigt for at fremskynde det.
\
Den eneste mulige kilde til denne stigning i energi er det arbejde, der udføres ved tryk for at skubbe væsken ind i den smalle del.
\
Så dette er arbejde, der udføres på vores klump af væske ved at væsken skubber den bagfra – men det er ikke slutningen på historien, fordi vores klump af væske selv virker ved at skubbe væsken foran den, så for at finde den samlede stigning i vores klods energi, skal vi trække det eksterne arbejde, det udfører, af.Det vil sige, at det samlede arbejde, der udføres ved at trykke på vores væske, er
\
at huske at \ (A_1v_1 = A_2v_2 \).
Dette udførte arbejde skal svare til ændringen i kinetisk energi, så
\
hvorfra
\
Dette er Bernoullis ligning.
\.
Bidragydere og tilskrivninger
- Michael Fowler (Beams Professor, Department of Physics, University of Virginia)