Úvod do nejbližších sousedů: výkonný algoritmus strojového učení (s implementací v Pythonu a R)

Poznámka: Tento článek byl původně publikován 10. října 2014 a aktualizován dne 27. března 2018

Přehled

• Pochopte k nejbližšího souseda (KNN) – jeden z nejpopulárnějších algoritmů strojového učení
• Naučte se pracovat s kNN v pythonu
• jednoduše si vyberte správnou hodnotu k

úvod

za čtyři roky své kariéry v oblasti datových věd jsem vytvořil více než 80% klasifikačních modelů a jen 15–20% regresních modelů. Tyto poměry lze víceméně zobecnit v celém odvětví. Důvodem této předpojatosti vůči klasifikačním modelům je, že většina analytických problémů zahrnuje rozhodování.

Bude například zákazník attrit nebo ne, pokud bychom měli cílit na zákazníka X pro digitální kampaně, ať už má zákazník vysoký potenciál či nikoli, atd. Tyto analýzy jsou důvtipnější a přímo souvisejí s implementačním plánem.

V tomto článku budeme hovořit o další široce používané techniky klasifikace strojového učení zvané K-nejbližší sousedé (KNN). Zaměříme se především na to, jak algoritmus funguje a jak vstupní parametr ovlivňuje výstup / predikci.

Poznámka: Lidé, kteří se raději učí prostřednictvím videí, se mohou naučit to samé prostřednictvím našeho bezplatného kurzu – K- Algoritmus nejbližších sousedů (KNN) v Pythonu a R. A pokud jste úplný začátečník v oblasti datové vědy a strojového učení, podívejte se na náš program Certified BlackBelt –

• Certified AI & Program ML Blackbelt +

Obsah

• Kdy použijeme algoritmus KNN?
• Jak funguje Funguje algoritmus KNN?
• Jak vybereme faktor K?
• Rozebrat to – Pseudokód KNN
• Implementace v Pythonu od nuly
• Porovnání našeho modelu s scikit-learn

Kdy použijeme algoritmus KNN?

KNN lze použít pro oba klasifikace a regrese prediktivní problémy. Více se však používá při klasifikačních problémech v průmyslu. Při hodnocení jakékoli techniky se obecně zaměřujeme na 3 důležité aspekty:

1. Snadno interpretovat výstup

2. Čas výpočtu

3. Prediktivní síla

Vezměme si několik příkladů, jak umístit KNN do stupnice:

Algoritmus KNN veletrhuje všechny parametry úvah. Běžně se používá pro snadnou interpretaci a nízkou dobu výpočtu.

Jak funguje algoritmus KNN?

Vezměme si jednoduchý případ pochopit tento algoritmus. Následuje šíření červených kruhů (RC) a zelených čtverců (GS):

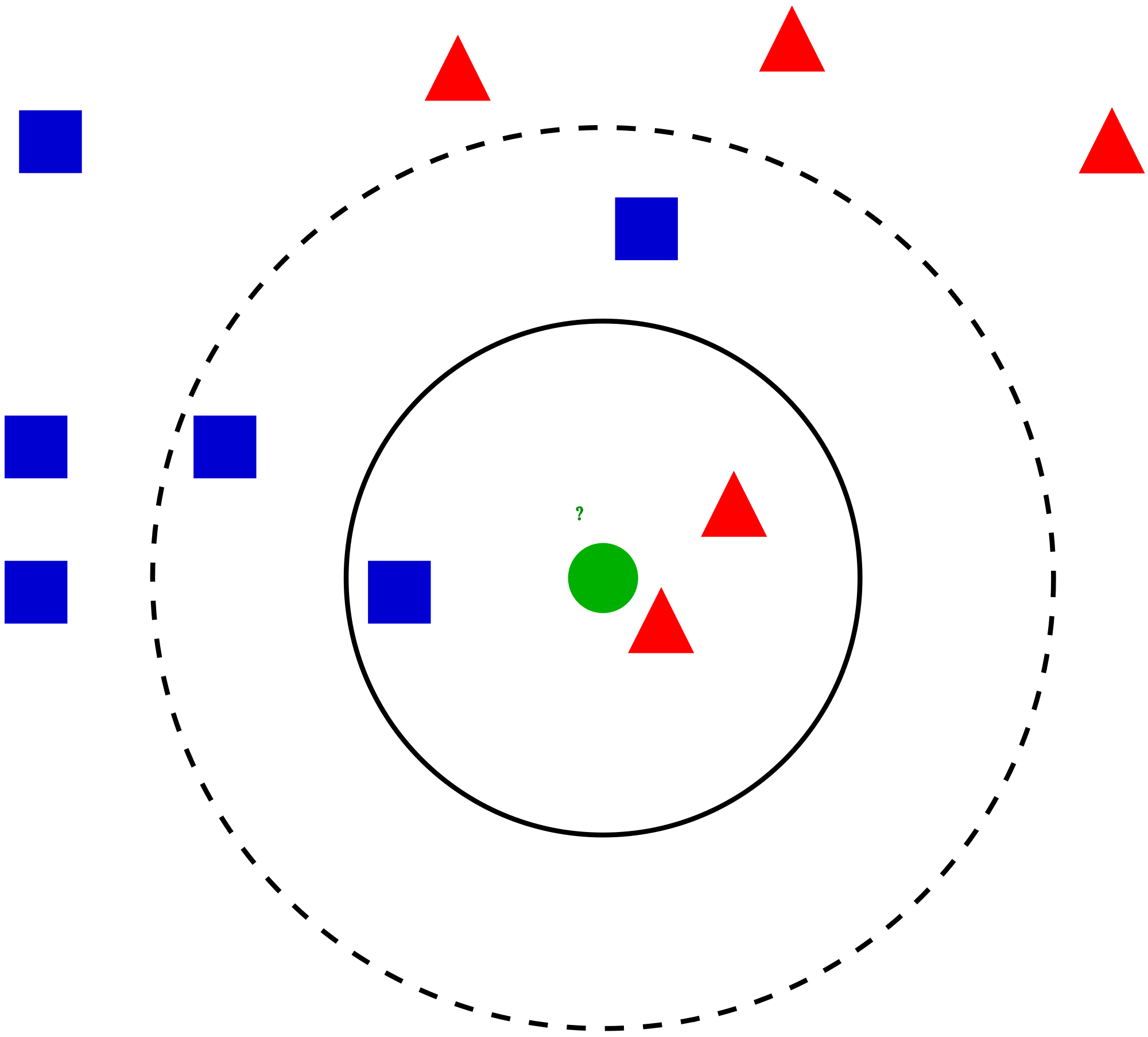
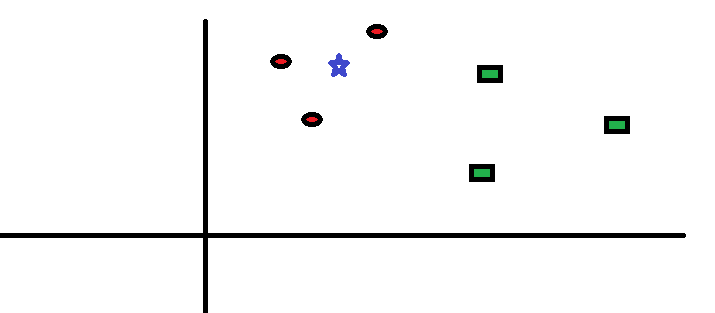Chcete to zjistit třída modré hvězdy (BS). BS může být RC nebo GS a nic jiného. Algoritmus „K“ je KNN je nejbližší soused, od kterého si přejeme hlasovat. Řekněme K = 3. Proto nyní vytvoříme kruh s BS jako středem tak velkým, jako je uzavření pouze tří datových bodů v rovině . Další podrobnosti najdete v následujícím diagramu:

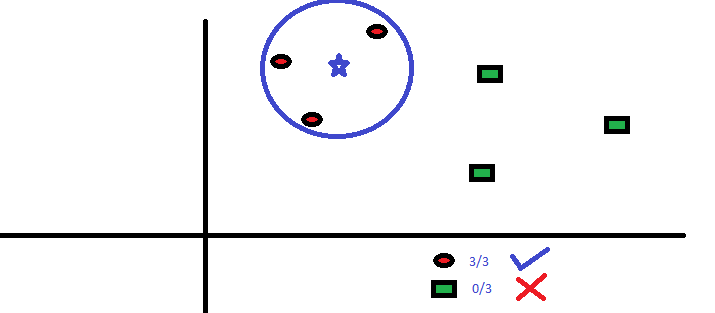Tři nejbližší body k BS jsou všechny RC. Proto, s dobrou úrovní spolehlivosti můžeme říci, že BS by měla patřit do třídy RC. Zde se volba stala velmi zřejmou, protože všechny tři hlasy od nejbližšího souseda šly do RC. Volba parametru K je v tomto algoritmu velmi důležitá . Dále pochopíme, jaké jsou faktory, které je třeba vzít v úvahu k dosažení nejlepší K.

Jak zvolíme faktor K?

Nejprve se pokusme pochopit, na co přesně má algoritmus vliv K. Pokud vidíme poslední příklad, vzhledem k tomu, že všech 6 tréninkových pozorování zůstává konstantní, s danou hodnotou K můžeme vytvořit hranice každé třídy. Hranice oddělují RC od GS. Stejným způsobem zkusme vidět vliv hodnoty „K“ na hranice tříd. Následují různé hranice oddělující dvě třídy s různými hodnotami K.

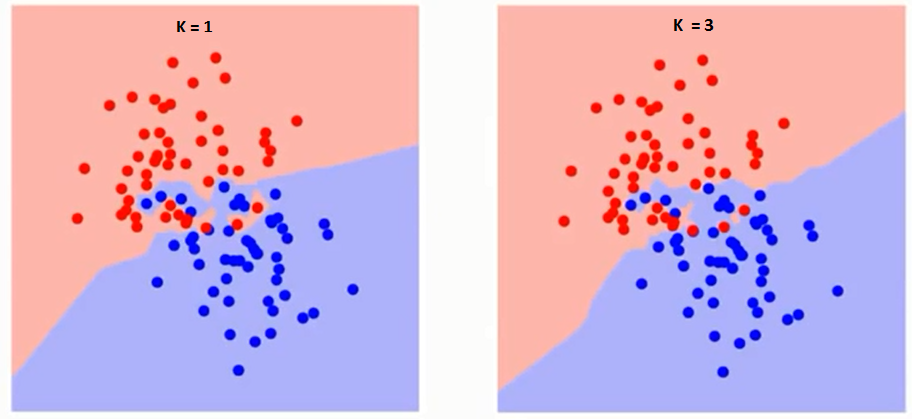
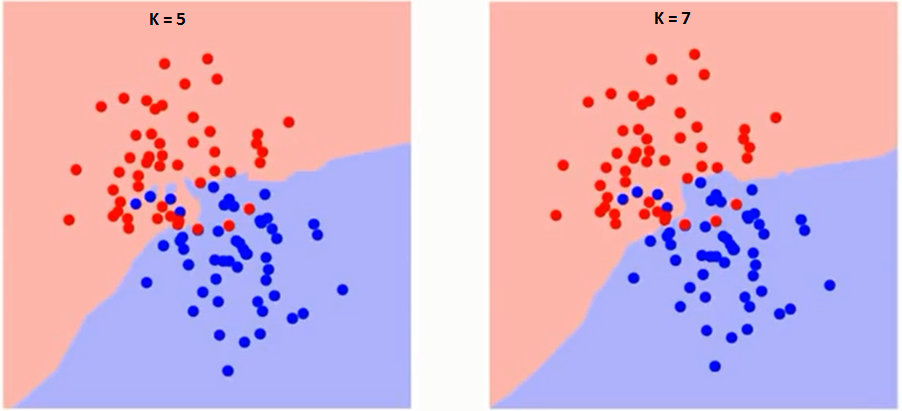
Pokud budete pečlivě sledovat, uvidíte, že hranice se stává hladší se zvyšující se hodnotou K. S rostoucím K do nekonečna se nakonec stane úplně modrá nebo celá červená v závislosti na celkové většině. Míra chyb při tréninku a míra chyb při ověřování jsou dva parametry, které potřebujeme pro přístup k různým hodnotám K. Následuje křivka pro míru chyb tréninku s různou hodnotou K:

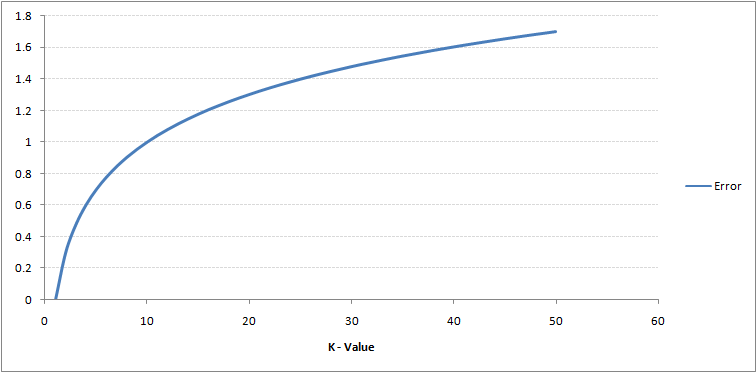Jak vidíte, chybovost při K = 1 je pro cvičný vzorek vždy nulová.Je to proto, že nejbližší bod k jakémukoli datovému bodu tréninku je sám o sobě. Proto je předpověď vždy přesná s K = 1. Pokud by křivka chyby validace byla podobná, naše volba K by byla 1. Následuje křivka chyby validace s různou hodnotou K:

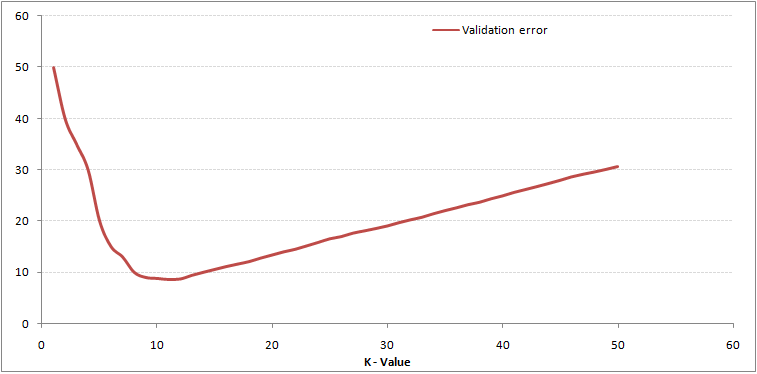Tím je příběh jasnější. Při K = 1 jsme překračovali hranice. Chybovost proto zpočátku klesá a dosahuje minim. Po bodu minima se pak zvyšuje s rostoucím K. Chcete-li získat optimální hodnotu K, můžete oddělit školení a ověření od počáteční datové sady. Nyní zakreslete křivku chyby ověření, abyste získali optimální hodnotu K. Tato hodnota K by měla být použita pro všechny předpovědi.

Výše uvedený obsah lze pochopit intuitivněji pomocí našeho bezplatného kurzu – K-Nejbližší sousedé ( KNN) Algoritmus v Pythonu a R

Rozdělení – Pseudokód KNN

Model KNN můžeme implementovat podle následujících kroků:

1. Načtěte data
2. Inicializujte hodnotu k
3. Pro získání předpokládané třídy proveďte iteraci od 1 do celkového počtu tréninkových datových bodů
   1. Vypočítejte vzdálenost mezi testem data a každý řádek tréninkových dat. Zde použijeme euklidovskou vzdálenost jako naši metriku vzdálenosti, protože je to nejoblíbenější metoda. Další metriky, které lze použít, jsou Čebyšev, kosinus atd.
   2. Seřadit vypočítané vzdálenosti ve vzestupném pořadí podle hodnot vzdáleností.
   3. Získat nejlepších k řádků z seřazeného pole
   4. Získejte nejčastější třídu těchto řádků
   5. Vrátí předpokládanou třídu

Implementace v Pythonu od nuly

K sestavení našeho modelu KNN budeme používat populární datovou sadu Iris. Můžete si jej stáhnout zde.

Porovnání našeho modelu s scikit-learn

Vidíme, že oba modely předpovídaly stejnou třídu (Iris- virginica ) a stejní nejbližší sousedé (). Můžeme tedy dojít k závěru, že náš model běží podle očekávání.

Implementace kNN v R

Krok 1: Import dat

Krok 2: Kontrola dat a výpočet souhrnu dat

Výstup

Krok 3: Rozdělení dat

Krok 4: Výpočet euklidovská vzdálenost

Krok 5: Zápis funkce pro predikci kNN

Krok 6: Výpočet štítku (Název) pro K = 1

Výstup

For K=1 "Iris-virginica"

Stejným způsobem můžete vypočítat i další hodnoty K.

Porovnání naší funkce prediktoru kNN s knihovnou „Class“

Výstup

For K=1 "Iris-virginica"

Vidíme, že oba modely předpovídaly stejnou třídu (Iris-virginica).

Koncové poznámky

KNN algoritmus je jedním z nejjednodušších klasifikačních algoritmů. I s taková jednoduchost, může poskytnout vysoce konkurenční výsledky. KNN algoritmus lze také použít pro regresní problémy. Jediný rozdíl z diskutované metodiky bude použití průměrů nejbližších sousedů spíše než hlasování od nejbližších sousedů. KNN lze kódovat v jednom řádku na R. Ještě musím prozkoumat, jak můžeme použít algoritmus KNN na SAS.

Považovali jste článek za užitečný? Použili jste v poslední době nějaký jiný nástroj pro strojové učení? Plánujete použít KNN při jakémkoli ze svých obchodních problémů? Pokud ano, podělte se s námi o to, jak to máte v plánu.

Pokud se vám líbí to, co jste právě četli, & chcete pokračovat v analytickém učení, přihlaste se k odběru našeho e-maily, sledujte nás na Twitteru nebo lajkněte naši facebookovou stránku.