A součet je výsledkem sčítání. Například přidáním 1, 2, 3 a 4 získáte součet 10, zapsáno
 |
(1)
|
Sčítaná čísla se nazývají sčítání nebo někdy sčítání. Operaci sčítání lze také indikovat pomocí kapitálového sigma s horní a dolní mezí zapsanou nad a pod a indexu označeného níže. Například lze napsat výše uvedený součet
 |
(2)
|
součet seznamu čísel je implementován jako Celkem.
Součet
 |
(3)
|
, ve kterém je každý výraz 
dán nějakým pevným pravidlem (tj. 
je studna -defined sequence) se nazývá (konečná) řada, a pokud je počet členů 
nekonečný, součet se nazývá nekonečná řada (nebo často jen „řada“). Součet tvaru
 |
(4)
|
se nazývá geometrická řada .
Podmínky pro konvergenci řady lze určit v jazyce Wolfram pomocí SumConvergence.
Obecný konečný mocninový součet
 |
(5)
|
lze zadat výrazem
 |
(6)
|
což je ekvivalent Faulhaberova vzorce, kde notace 
znamená množství v otázka je položena na příslušnou moc 
a všechny výrazy ve tvaru 
jsou nahrazeny odpovídajícími Bernoulliho čísla 
.
Zábavná identita J. Ziegenbeina (pers. Comm., 19. června 2002) vyplývá z identity
 |
(7)
|
které lze zapsat
 |
(8)
|
Proto 
lze například psát v ekvivalentních formách
 |
 |
 |
(9)
|
 |
 |
 |
(10)
|
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
a tak dále.
Nicomachova věta udává jako kuriózní výraz pro výkonový součet 
.
Zvláštní částky zahrnují
 |
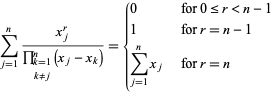(13)
|
a
 |
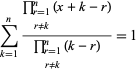(14)
|
Chcete-li minimalizovat součet množiny čtverců čísel 
o daném počtu 
 |
 |
 |
(15 )
|
 |
 |
 |
(16)
|
převzít derivát.
 |
(17)
|
Řešení pro 
dává
 |
(18)
|
takže 
je minimalizován, když je 
nastaven na zlý.