Zvonková křivka, známá také jako normální rozdělení, je nejběžnějším typem rozdělení proměnné. Je přijímán jako distribuce, která se přirozeně vyskytuje v mnoha situacích. Ve zvonové křivce definuje nejvyšší bod oblouku průměr, což je nejvyšší počet výskytů prvku. Pravděpodobnost výskytu klesá směrem k jedné straně křivky. Zvonovou křivku můžete použít k porovnání výkonů vyloučením extrémů nebo definováním svých očekávání možností, že výsledek bude ležet v rozmezí nalevo nebo napravo od středu. V této příručce vám ukážeme, jak vytvořit křivku zvonu v aplikaci Excel s příkladem použití v reálném světě.
Stáhnout sešit
Základy
Vše, co potřebujete, je průměr (průměr) a hodnoty standardní odchylky vaší datové sady. Obě tyto metriky lze v aplikaci Excel vypočítat pomocí níže uvedených vzorců.
S ohledem na tyto dvě hodnoty se normálně distribuované hodnoty řídí těmito pravidly:
- Celková plocha pod křivka se rovná 1 (100%)
- Střed zvonové křivky je průměrem datového bodu
- (1-σ) Asi 68,2% plochy pod křivkou spadá do jedné směrodatné odchylky (průměr ± standardní odchylka)
- (2-σ) Asi 95,5% plochy pod křivkou spadá do dvou směrodatných odchylek (průměr ± 2 * standardní odchylka)
- (3-σ) Asi 99,7% plochy pod křivkou spadá do tří směrodatných odchylek (průměr ± 3 * směrodatná odchylka)
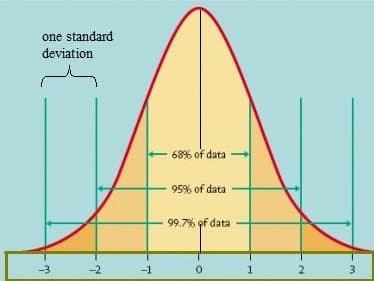
Obrázek z University of Virginia
Vytvoření křivky zvonu v aplikaci Excel
Vezměme si běžný příklad a řekněme, že analyzujeme výsledky zkoušky lts pro třídu studentů. Budeme používat zvonovou křivku k měření výsledků zkoušek pro lepší srovnání.
Začneme výpočtem metrik, abychom vygenerovali normální distribuovaná data, která vygenerují naši křivku. Musíme vypočítat:
- Průměr (průměr) hodnot.
- Směrodatná odchylka hodnot.
- Limity standardní odchylky pro dříve a po střední hodnotě.
- Intervalová hodnota pro normálně distribuované datové body. To také vyžaduje určení intervalových bodů. Můžete vybrat libovolné číslo, ale nezapomeňte, že více intervalů znamená větší přesnost.
Metriky
Začněte výpočtem střední a standardní odchylky dat. Pomocí funkcí AVEREAGE a STDEV.P můžete vypočítat hodnoty střední a standardní odchylky.

Dalším krokem je výpočet 3 hodnoty standardní odchylky pro nastavení minimální a maximální hodnoty pro 99,7% dat.

Maximum = 83,23 – 3 * 5,54 = 99,86
Po nastavení minimální a maximální hodnoty pro naši křivku musíme vygenerovat intervaly . Hodnoty intervalu budou základem pro normálně distribuované hodnoty. Chcete-li vypočítat intervaly, musíte pouze rozdělit oblast mezi minimální a maximální hodnotou počtem intervalů. V tomto příkladu jsme to nastavili na 20, ale můžete použít větší číslo ke zvýšení počtu datových bodů.

Jakmile je hodnota intervalu vypočítána, můžete vygenerovat datové body. Chcete-li to provést, zadejte minimální hodnotu do buňky. Potom přímo pod minimální hodnotu zadejte vzorec a přidejte hodnotu intervalu na minimum. Zde jsme použili odkazy na buňky (například jako J4), které pomáhají snadno naplnit datové body až na maximální hodnotu.

Dalším krokem je výpočet normálně distribuovaných hodnot z vygenerovaných datových bodů. K vygenerování těchto hodnot můžete použít funkci Excel NIST.DIST.
Vyplněné datové body použijte jako první argument funkce. Hodnoty střední a standardní odchylky jsou další argumenty. Dokončete vzorec FALSE Boolean hodnotou, abyste použili nekumulativní typ této funkce.

Graf
Jsme téměř hotoví! Vyberte datové body a hodnoty normálního rozdělení a poté vložte bodový graf X-Y. Pomocí verze Scattered with Smooth Lines vytvořte křivku zvonu v aplikaci Excel.

Graf se může zdát nejprve trochu vypnutý.Podívejme se, jak jej můžete vylepšit.
Chcete-li změnit název grafu, poklepejte na název a název aktualizujte.
Dále poklepejte na Osa X a definujte minimální a maximální hodnoty z panelu Možnosti osy, abyste odstranili prázdné místo na obou stranách. Díky tomu bude mít váš graf lepší tvar zvonu. Nastavili jsme hodnoty, které jsou trochu mimo naši datovou sadu. Například 66 – 100 pro hodnoty 66,30 – 99,86.
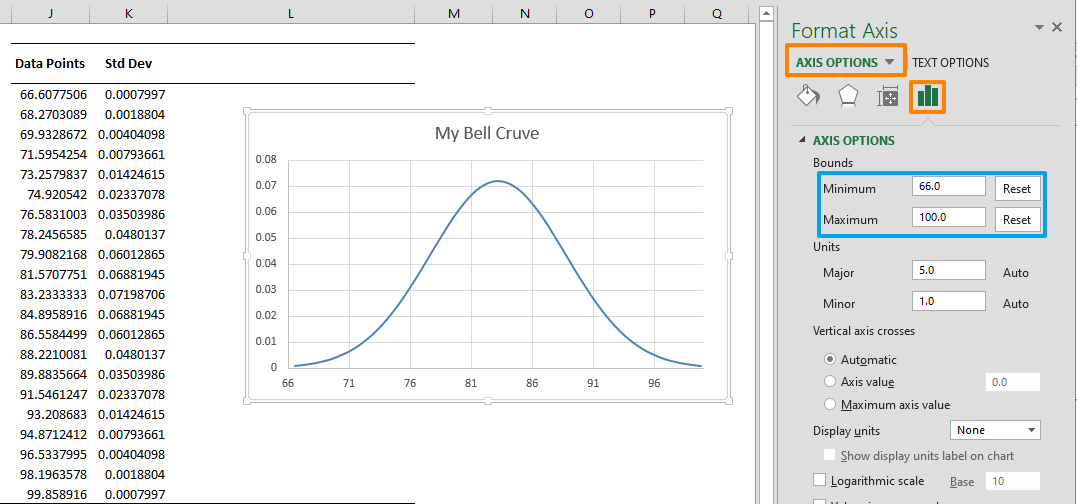
Graf můžete dále vylepšit přidáním hodnot standardní odchylky .
