Sklon
Kromě známého významu má slovo „sklon“ i přesný matematický význam. Sklon přímky je vzestup běhu nebo změna y dělená změnou x. Chcete-li zjistit sklon přímky, vyberte libovolné dva body na přímce. Pak odečtěte jejich souřadnice x a odečtěte jejich souřadnice y ve stejném pořadí. Vydělte rozdíl souřadnic y rozdílem souřadnic x:
Vzhledem ke dvěma bodům (x1, y1) a (x2, y2) na přímce se sklon čáry rovná:
m = =
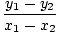
Negativní sklon
Pokud má čára kladný sklon (tj. m > 0), pak y vždy roste, když x roste a y vždy klesá, když x klesá. Graf čáry tedy začíná vlevo dole a směřuje vpravo nahoře.
Sklon čáry je však často záporný. Záporný sklon znamená, že y vždy klesá, když x roste a y se vždy zvyšuje, když x klesá. Zde je příklad grafu se záporným sklonem:
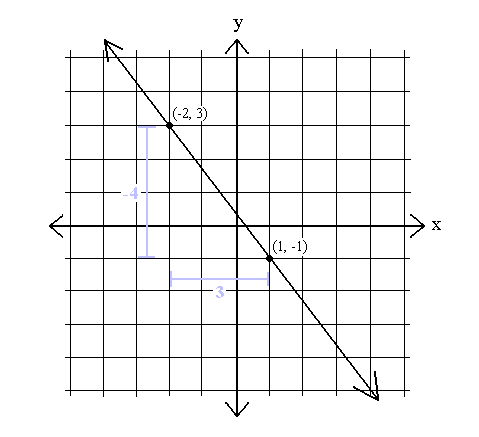
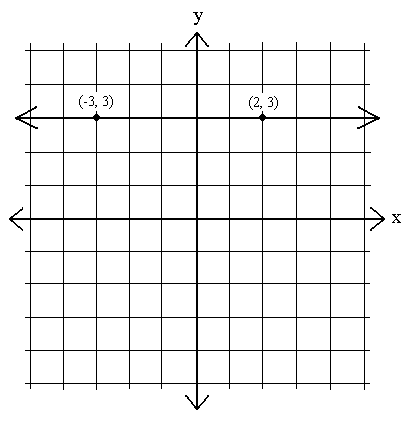
m =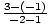 
= 
= – 
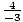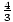
Tedy jak x roste o 3, y klesá o 4 a jak x klesá o 3, y roste o 4.
Vodorovné a svislé čáry
Někdy , uvidíme rovnice, jejichž grafy jsou vodorovné čáry. Jedná se o grafy, ve kterých y zůstává konstantní – tj. Ve kterých y1 – y2 = 0 pro libovolné dva body na řádku:
m =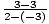 
= 
= 0.
Sklon libovolné vodorovné čáry je 0. Jinými slovy, jak se x zvyšuje nebo snižuje, y se nemění. x vezme každou možnou hodnotu při konkrétní hodnotě y.
Uvidíme také rovnice, jejichž grafy jsou svislé čáry. Jedná se o grafy, ve kterých x zůstává konstantní – tj. Ve kterém x1 – x2 = 0 pro libovolné dva body na řádku:
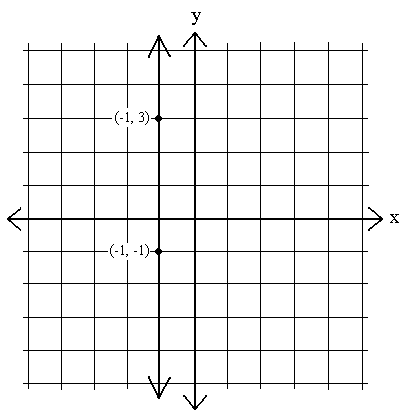
m =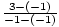 
= 
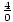= nedefinováno. Číslo nemůžeme vydělit nulou.
Sklon libovolné svislé čáry je nedefinovaný. X se nezvyšuje ani nesnižuje; spíše y bere každou možnou hodnotu při konkrétní hodnotě x.