Co je BFS Algorithm (Breadth-First Search)?
Breadth-first search (BFS) je algoritmus, který se používá ke grafování dat nebo prohledávání stromu nebo procházení struktur. Plnou formou BFS je vyhledávání na šířku.
Algoritmus efektivně navštíví a označí všechny klíčové uzly v grafu přesnou šířkou. Tento algoritmus vybere v grafu jeden uzel (počáteční nebo zdrojový bod) a poté navštíví všechny uzly sousedící s vybraným uzlem. Nezapomeňte, že BFS přistupuje k těmto uzlům jeden po druhém.
Jakmile algoritmus navštíví a označí počáteční uzel, posune se k nejbližším nenavštíveným uzlům a analyzuje je. Po návštěvě jsou označeny všechny uzly. Tyto iterace pokračují, dokud nebudou úspěšně navštíveny a označeny všechny uzly grafu.
V tomto výukovém programu Algoritmus se naučíte:
- Co je to BFS Algorithm (vyhledávání podle šířky)?
- Co je to Graph Traversals?
- Architektura BFS algoritmu
- Proč potřebujeme BFS Algorithm?
- Jak funguje BFS Algorithm?
- Příklad BFS Algorithm
- Pravidla BFS Algorithm
- Aplikace BFS Algorithm
Co je to Graph Traversals?
Traverz grafu je běžně používaná metodika pro lokalizaci polohy vrcholu v grafu. Jedná se o pokročilý vyhledávací algoritmus, který dokáže analyzovat graf s rychlostí a přesností spolu s vyznačením sekvence navštívených vrcholů. Tento proces umožňuje rychle navštívit každý uzel v grafu, aniž byste byli uzamčeni v nekonečné smyčce.
Architektura algoritmu BFS
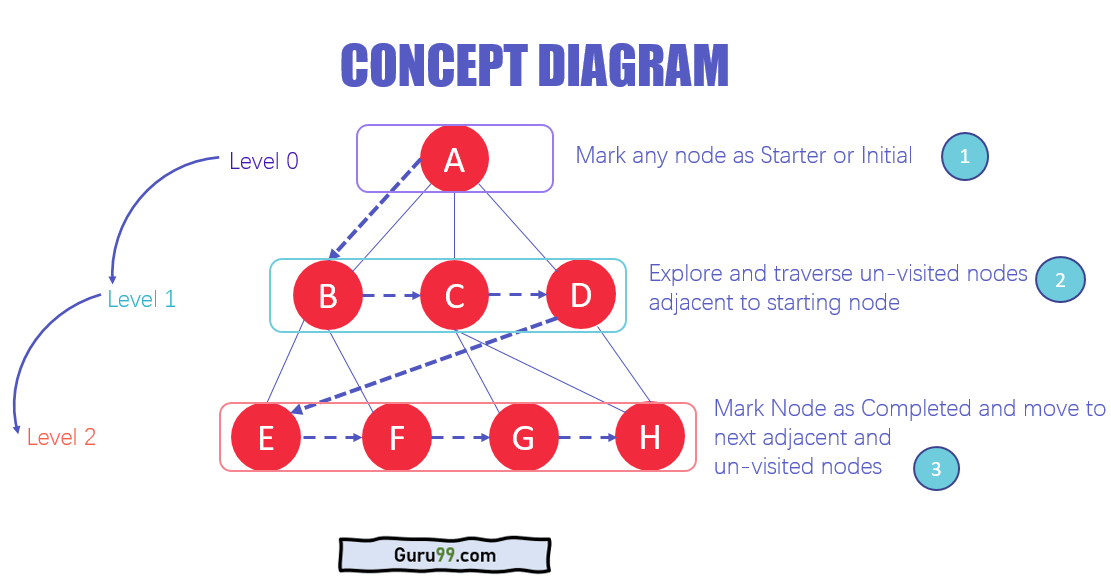
- Na různých úrovních dat můžete označit libovolný uzel jako výchozí nebo počáteční uzel k zahájení procházení. BFS navštíví uzel a označí jej jako navštívený a umístí jej do fronty.
- Nyní BFS navštíví nejbližší a nenavštívené uzly a označí je. Tyto hodnoty se také přidají do fronty. Fronta funguje na modelu FIFO.
- Podobným způsobem jsou zbývající nejbližší a nenavštívené uzly v grafu analyzovány, označeny a přidány do fronty. Tyto položky jsou odstraněny z fronty jako přijaté a vytištěny jako výsledek.
Proč potřebujeme Algoritmus BFS?
Existuje mnoho důvodů, proč použít Algoritmus BFS k vyhledání vaší datové sady. Některé z nejdůležitějších aspektů, díky nimž je tento algoritmus vaší první volbou, jsou:
- BFS je užitečný pro analýzu uzlů v grafu a konstrukci nejkratší cesty jejich procházení.
- BFS může procházet grafem v nejmenším počtu iterací.
- Architektura algoritmu BFS je jednoduchá a robustní.
- Výsledek algoritmu BFS má ve srovnání s jinými algoritmy vysokou úroveň přesnosti.
- BFS iterace jsou bezproblémové a není možné, aby se tento algoritmus dostal do problému nekonečné smyčky.
Jak funguje BFS Algorithm?
Procházení grafu vyžaduje, aby algoritmus navštívil, zkontroloval nebo aktualizoval každý jednotlivý nenavštívený uzel ve stromové struktuře. Procházení grafů je kategorizováno podle pořadí, ve kterém navštíví uzly v grafu.
Algoritmus BFS spouští operaci od prvního nebo počátečního uzlu v grafu a důkladně ji prochází. Jakmile úspěšně projde počátečním uzlem, je navštíven a označen další neprocházející vrchol v grafu.
Proto můžete říci, že všechny uzly sousedící s aktuálním vrcholem jsou navštíveny a procházeny v první iteraci. K implementaci práce s algoritmem BFS se používá jednoduchá metodologie fronty, která se skládá z následujících kroků:
Krok 1)

Každý vrchol nebo uzel v grafu je známý. Například můžete uzel označit jako V.
Krok 2)

Pokud není přístup k vrcholu V, přidejte vrchol V do fronty BFS
Krok 3)

Spusťte vyhledávání BFS a po dokončení označte vrchol V jako navštívený.
Krok 4)

Fronta BFS je stále není prázdný, proto odstraňte vrchol V grafu z fronty.
Krok 5)

Načíst všechny zbývající vrcholy na grafu, který sousedí s vrcholem V
Krok 6)

Pro každý sousední vrchol řekněme V1, pokud ještě není navštíven, přidejte V1 do fronty BFS
Krok 7)

BFS navštíví verzi V1, označí ji jako navštívenou a odstraní ji z fronty.
Příklad algoritmu BFS
Krok 1)

Máte graf sedm čísel v rozmezí od 0 do 6.
Krok 2)

0 nebo nula byla označena jako kořenový uzel.
Krok 3)

0 je navštíveno, označeno a vloženo do datové struktury fronty.
Krok 4)
Zbývající 0 sousedních a nenavštívených uzlů je navštíveno, označeno a vloženo do fronty.
Krok 5)

Traverské iterace se opakují, dokud nenavštívíte všechny uzly.
Pravidla algoritmu BFS
Zde jsou důležitá pravidla pro používání algoritmu BFS:
- Datová struktura fronty (FIFO-první od prvního) je používán BFS.
- Označíte libovolný uzel v grafu jako root a začnete z něj procházet data.
- BFS prochází všechny uzly v grafu a stále je vypouští jako dokončené.
- BFS navštíví sousední nenavštívený uzel, označí jej jako hotový a vloží jej do fronty.
- Odstraní předchozí vrchol z fronty v případě, že nebude nalezen žádný sousední vrchol.
- Algoritmus BFS iteruje, dokud nebudou všechny vrcholy v grafu úspěšně překonány a označeny jako dokončené.
- Neexistují žádné smyčky způsobené BFS během procházení dat z libovolného uzlu.
Aplikace algoritmu BFS
Pojďme podívejte se na některé aplikace v reálném životě, kde implementace algoritmu BFS může být vysoce efektivní.
- Nevážené grafy: Algoritmus BFS může snadno vytvořit nejkratší cestu a minimální strom, který by mohl navštívit všechny vrcholy grafu v co nejkratším čase s vysokou přesností.
- P2P sítě: BFS lze implementovat tak, aby lokalizoval všechny nejbližší nebo sousední uzly v síti typu peer to peer. Tím rychleji vyhledáte požadovaná data. .
- Webové prohledávače: Vyhledávací stroje nebo webové prohledávače mohou snadno vytvářet více úrovní indexů pomocí BFS. Implementace BFS začíná od zdroje, kterým je webová stránka, a poté navštíví všechny odkazy z tohoto zdroje. .
- Navigační systémy: BFS může pomoci najít všechna sousední místa z hlavního nebo zdrojového umístění.
- Network Broadcast ing: Vysílaný paket je veden algoritmem BFS k nalezení a dosažení všech uzlů, pro které má adresu.
Shrnutí
- Procházení grafu je jedinečný proces, který vyžaduje, aby algoritmus navštívil, zkontroloval a / nebo aktualizoval každý jeden nenavštívený uzel v stromová struktura. Algoritmus BFS funguje na podobném principu.
- Algoritmus je užitečný pro analýzu uzlů v grafu a konstrukci nejkratší cesty jejich procházení.
- Algoritmus prochází grafem v nejmenším počtu iterací a v co nejkratším čase.
- BFS vybere v grafu jeden uzel (počáteční nebo zdrojový bod) a poté navštíví všechny uzly sousedící s vybraným uzlem. BFS přistupuje k těmto uzlům jeden po druhém.
- Navštívená a označená data jsou umístěna do fronty BFS. Fronta funguje od prvního do prvního. Proto je prvek umístěný v grafu jako první odstraněn jako první a vytištěn jako výsledek.
- Algoritmus BFS se nikdy nemůže zachytit v nekonečné smyčce.
- Díky vysoké přesnosti a robustní implementaci se BFS používá v mnoha reálných řešeních, jako jsou sítě P2P, webové prohledávače, a síťové vysílání.