Jak se mění tlak při změně objemu během adiabatické expanze a komprese v ideálním plynu? Tato stránka je přílohou naší diskuse o zvuku. Vzduch za atmosférického tlaku je téměř ideální plyn a přenos zvuku ve vzduchu je pro normální frekvence a přenosové vzdálenosti blízký adiabatickému. (K tomuto předpokladu se vrátíme níže.)
První zákon termodynamiky souvisí se změnou vnitřní energie dU s prací dW provedenou systémem a přidáním tepla dQ.
dU = dQ – dW
Podle definice v adiabatickém procesu si teplo vyměnilo dQ = 0. Nahrazením tohoto v prvním zákoně a přeskupením získáte
0 = dQ = dU + dW
Druhý termín je snadný: práce provedená dW, když systém změní svůj objem V o dV, je PdV.
První termín může souviset se specifickým teplem, které je definováno jako teplo přidané na jednotku změny teploty na mol látky. Přidáme-li teplo při konstantním objemu, plyn se neroztahuje a tak to nefunguje. Přidané teplo tedy zvyšuje vnitřní energii U. Z toho tedy vyplývá, že specifické teplo při konstantním objemu je ![]() , kde n je počet molů.
, kde n je počet molů.
Stavová rovnice ideálního plynu je nyní
nRT = PV ( ii)
kde R je plynová konstanta. Převzetí derivátů dává
Nyní můžeme kombinovat rovnice (i) a (iii), abychom eliminovali T. (i) a (ii) uveďte pro ncv dT tyto výrazy:
Shromáždění výrazů PdV a VdP dává
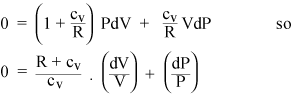
Pokud je plyn ideální, jeho vnitřní energie je celá kinetická, takže vnitřní energie U závisí pouze na T. Ze stavové rovnice ideálního plynu (ii) můžeme vypočítat práce dW prováděná při konstantním tlaku: je to jen PdV = nRdT. Pokud tedy přidáme teplo do plynu za konstantního tlaku, musíme extrahovat RdT pro každý mol plynu, nad rámec tepla, které bychom měli přidat při stálém objemu. Takže měrné teplo ideálního plynu při konstantním tlaku je pouze cP = cv + R. Poměru měrných ohřevů je přiřazen standardní symbol:
. Takže máme
(iv)
Toto je hlavní výsledek, o kterém musíme diskutovat o zvukových vlnách: právě jsme ukázali, že proporcionální změna tlaku je – γ krát proporcionální změna objemu nebo γ krát proporcionální změna hustoty.
Nezastavme se však zde, protože nás dělí jen pár řádků od důležitého výsledku. Víme, že d (ln x) = dx / x (důkaz najdete v kalkulu). Můžeme tedy psát předchozí rovnice jako
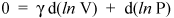
a přeskupte jej tak, aby měl
(v)
Proto pro adiabatický proces v ideálním plynu,
. (vi)
Na základě zamyšlení souhlasíte s tím, že cP > cV: v konstantní objem, všechny tis Vložené teplo jde ke zvýšení vnitřní energie a tím ke zvýšení teploty. Při konstantním tlaku musíte vložit nejen teplo, které zvyšuje vnitřní energii, ale také množství tepla, které se rovná práci provedené, když systém prochází tepelnou roztažností. Pro vzduch je γ asi 1,4.
Samozřejmě můžeme nyní dosadit do (vi) ze stavové rovnice (ii), abychom viděli, jak P a T nebo T a V souvisejí s adiabatickým procesem.
Kdy je zvuk adiabatický?
Výše jsme zmínili, že „přenos zvuku ve vzduchu je pro normální frekvence a přenosové vzdálenosti blízký adiabatickému“. Kdy to selže? Při maximu tlaku ve zvukové vlně je teplota vysoká. Očekáváme tedy, že určité teplo bude difundovat do sousedních tlakových minim. Samozřejmě za polovinu periody zvukové vlny není mnoho času na to, aby teplo rozptýlilo jednu polovinu vlnové délky. Avšak doba potřebná k rozptýlení tepla jde jako čtverec vzdálenosti. Tento proces je tedy pro vysoké frekvence méně zanedbatelný, protože kratší poloviční vlnová délka více než kompenzuje kratší poloviční periodu. Tato difúze bere mechanickou energii z vlny, zejména při vysokých frekvencích, a účinek se zvyšuje s přenosovou vzdáleností.Z tohoto důvodu (a někdy i dalších) jsou vzdálené zvuky nejen méně hlasité, ale také méně jasné než zvuky blízké.