Vztah mezi tlakem a objemem: Boyleův zákon
Se zvyšujícím se tlakem na plyn se objem plynu zmenšuje, protože částice plynu jsou tlačeny blíže k sobě. Naopak, jak klesá tlak na plyn, zvyšuje se objem plynu, protože částice plynu se nyní mohou pohybovat dále od sebe. Meteorologické balóny se zvětšují, jak stoupají atmosférou do oblastí s nižším tlakem, protože se zvýšil objem plynu; to znamená, že atmosférický plyn vyvíjí menší tlak na povrch balónu, takže vnitřní plyn expanduje, dokud nejsou vnitřní a vnější tlaky stejné.
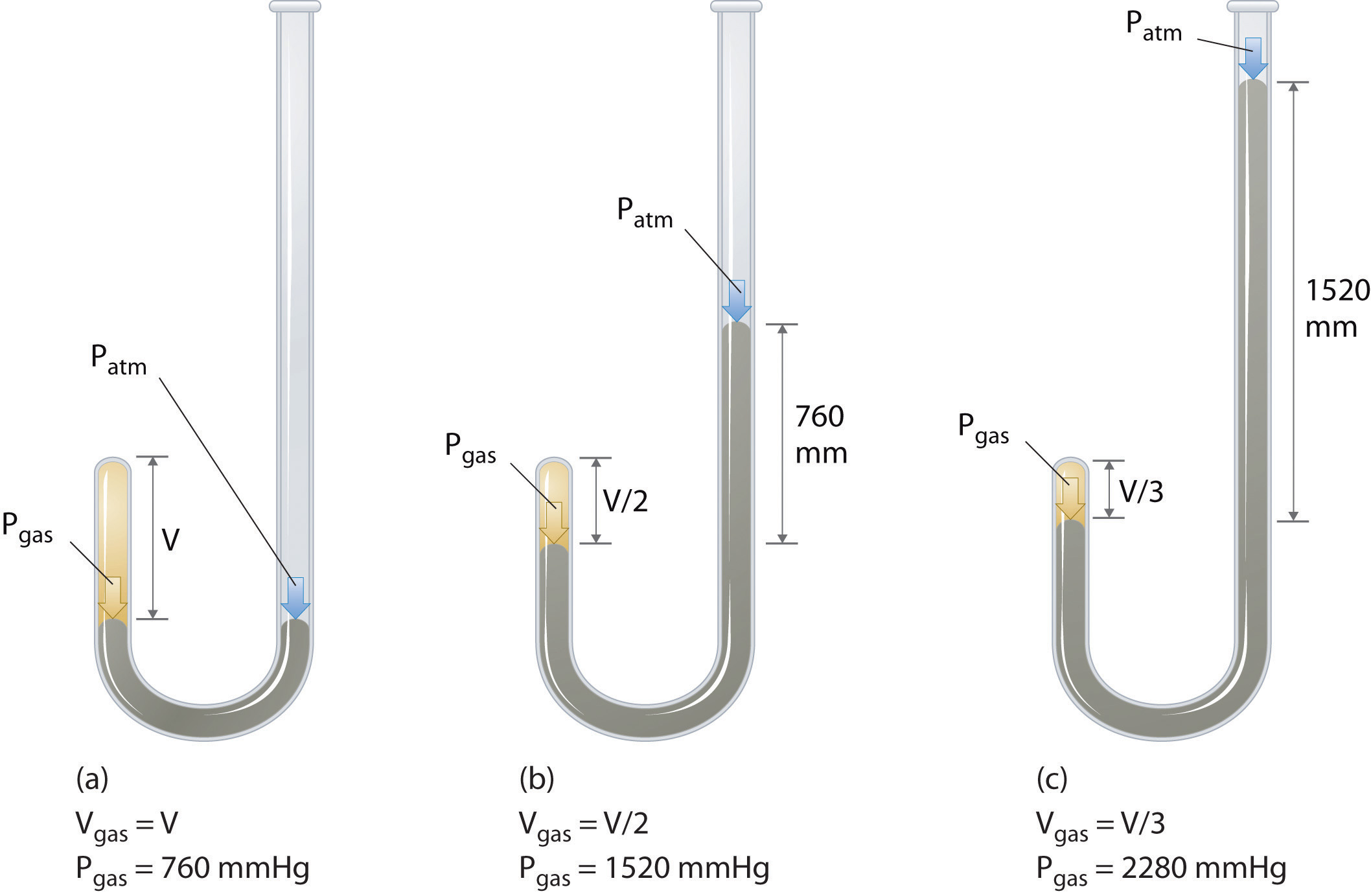
Irský chemik Robert Boyle (1627–1691) provedl některé z prvních experimentů, které určovaly kvantitativní vztah mezi tlakem a objemem benzín. Boyle použil trubku ve tvaru J částečně naplněnou rtutí, jak je znázorněno na obrázku \ (\ PageIndex {1} \). V těchto experimentech je malé množství plynu nebo vzduchu zachyceno nad rtuťovým sloupcem a jeho objem je měřen při atmosférickém tlaku a konstantní teplotě. Poté se do otevřeného ramene nalije více rtuti, aby se zvýšil tlak na vzorek plynu. Tlak na plyn je atmosférický tlak plus rozdíl ve výškách rtuťových kolon a změří se výsledný objem. Tento proces se opakuje, dokud v otevřeném rameni již není žádný prostor, nebo dokud není objem plynu příliš malý na to, aby se dal přesně měřit. Data, jako jsou data z jednoho z Boyleových vlastních experimentů, lze vykreslit několika způsoby (obrázek \ (\ PageIndex {2} \)). Jednoduchý graf \ (V \) versus \ (P \) dává křivku zvanou hyperbola a odhaluje inverzní vztah mezi tlakem a objemem: při zdvojnásobení tlaku se objem sníží dvakrát. Tento vztah mezi těmito dvěma veličinami je popsán následovně:
\
Vydělením obou stran \ (P \) získáme rovnici ilustrující inverzní vztah mezi \ (P \) a \ (V \):
\
nebo
\
, kde se čte symbol „„ je úměrný “. Graf V proti 1 / P je tedy přímka, jejíž sklon se rovná konstantě v Rovnicích \ (\ ref {10.3.1} \) a \ (\ ref {10.3.3} \). Dělení obou stran Rovnice \ (\ ref {10.3.1} \) pomocí V místo P dává podobný vztah mezi P a 1 / V. Číselná hodnota konstanty závisí na množství plynu použitého v experimentu a na teplotě, při které experimenty jsou prováděny. Tento vztah mezi tlakem a objemem je po svém objeviteli znám jako Boyleův zákon a lze jej vyjádřit následovně: Při konstantní teplotě je objem stálého množství plynu nepřímo úměrný jeho tlaku. Zákon v praxi je znázorněn na obrázku \ (\ PageIndex {2} \).
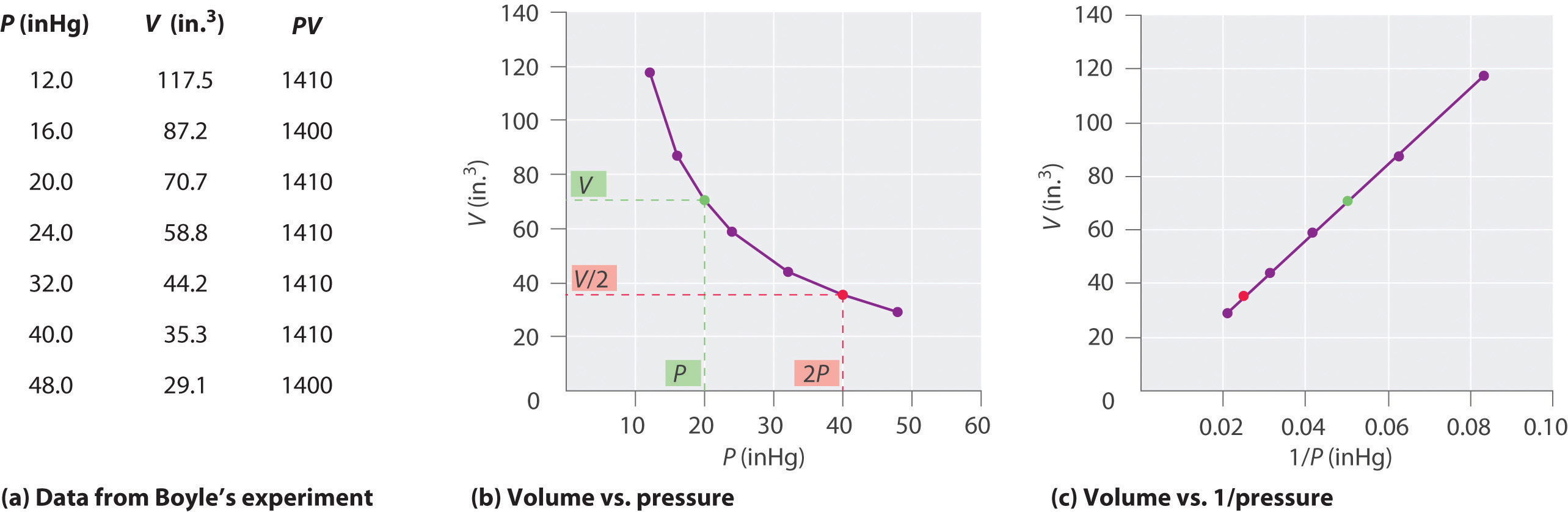
Při konstantní teplotě je objem stálého množství plynu nepřímo úměrný jeho tlaku