Při provádění zbytkové analýzy je nejčastěji vytvářeným grafem „reziduální versus vyhovující graf“. Jedná se o bodový graf reziduí na ose y a přizpůsobené hodnoty (odhadované odpovědi) na ose x. Děj se používá k detekci nelinearity, nerovnoměrných odchylek chyb a odlehlých hodnot.
Pojďme se podívat na příklad, abychom viděli, jak vypadá „dobře vychovaný“ zbytkový graf. Někteří vědci (Urbano- Marquez a kol., 1989) se zajímali o to, zda konzumace alkoholu přímo souvisí se svalovou silou. Vědci měřili celkovou celoživotní konzumaci alkoholu (x) na náhodném vzorku n = 50 alkoholiků. síla (y) deltového svalu v nedominantní paži každého člověka. Upravený spojnicový graf výsledných dat (alcoholarm.txt) vypadá takto:
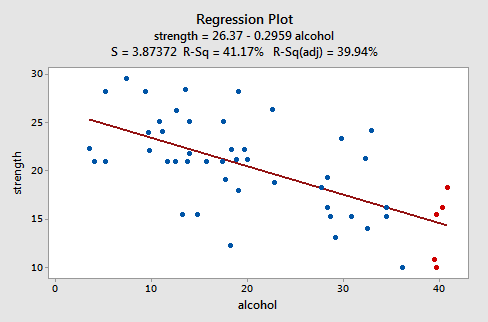
Děj naznačuje, že mezi alkoholem a silou paží klesá lineární vztah. Také to naznačuje, že v datové sadě nejsou žádné neobvyklé datové body. A ilustruje, že variace kolem odhadované regresní přímky je konstantní, což naznačuje, že předpoklad stejných odchylek chyb je přiměřený.
Zde vypadá odpovídající graf reziduí versus fit pro soubor dat jednoduchý lineární regresní model se silou paže jako odpovědí a úrovní konzumace alkoholu jako prediktorem:
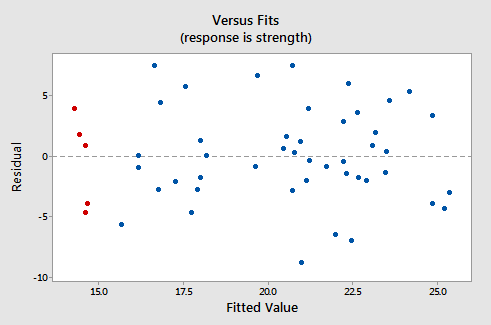
Všimněte si, že podle definice se zbytky objeví na ose y a přizpůsobené hodnoty na ose x. Měli byste být schopni ohlédnout se za bodovým grafem dat a zjistit, jak tam datové body odpovídají datovým bodům v grafu zbytkové versus fit zde. Pokud s tím nemáte potíže, podívejte se na pět datových bodů v původním rozptylovém grafu, které se zobrazují červeně. Všimněte si, že předpokládaná odpověď (přizpůsobená hodnota) těchto mužů (jejichž spotřeba alkoholu je kolem 40) je asi 14 . Všimněte si také vzoru, ve kterém se pět datových bodů odchyluje od odhadované regresní přímky.
Nyní se podívejte na to, jak a kde se těchto pět datových bodů objeví v grafu rezidua versus fit. Jejich přizpůsobená hodnota je asi 14 a jejich odchylka od čáry zbytkové = 0 sdílí stejný vzorec jako jejich odchylka od odhadované regresní čáry. Vidíte spojení? Jakýkoli datový bod, který spadá přímo na odhadovanou regresní čáru, má zbytkovou hodnotu 0. Proto zbytková = Řádek 0 odpovídá odhadované regresní přímce.
Tento graf je klasickým příkladem dobře vychovaného zbytkového vs. vhodného grafu. Zde jsou charakteristiky dobře vychovaného zbytkového vs. vhodného grafu a jaké jsou naznačují vhodnost jednoduchosti Model lineární regrese:
- Rezidua „náhodně odskočí“ kolem 0 řádku. To naznačuje, že předpoklad, že vztah je lineární, je rozumný.
- Rezidua zhruba tvoří kolem čáry 0 „vodorovný pás“. To naznačuje, že odchylky chybových podmínek jsou stejné.
- Nikdo zbytkový „nevyčnívá“ ze základního náhodného vzoru zbytků. To naznačuje, že neexistují žádné odlehlé hodnoty.
Obecně chcete, aby vaše zbytkové vs. vhodné grafy vypadaly podobně jako výše uvedený graf. Nezapomeňte však, že interpretace těchto zápletek je subjektivní. Moje zkušenost je, že studenti, kteří se poprvé učí reziduální analýzu, mají tendenci tyto zápletky nadměrně interpretovat a dívat se na každý zvrat a obracet se jako na něco potenciálně problematického. dávejte pozor, abyste příliš nezatěžovali zbytkové vs. záchytné grafy založené na malých souborech dat. Někdy jsou datové soubory příliš malé na to, aby interpretace zbytkového vs. záchvatového diagramu stála za to. Nedělejte si starosti! Naučíte se – s praxí – jak „číst“ tyto grafy.