1.3: Bernoulliho efekt

Předpokládejme, že vzduch je čerpán do hladké kulaté trubice, která má konstantní průměr, s výjimkou části uprostřed, kde se trubice zužuje až na polovinu průměru, poté se opět rozšiřuje. Předpokládejme, že všechny změny v průměru probíhají hladce a vzduch plynule proudí dolů trubicí, bez víření a turbulencí.

Abychom zjistili, jak by to mohlo být, použijeme techniky, které jsme vyvinuli, abychom zjistili, jak se mění tlak ve stacionární tekutině. Způsob, jakým jsme to udělali, pamatujte, bylo nakreslení diagramu volného těla pro malý válec tekutiny. Vzhledem k tomu, že tento malý válec byl v klidu, celková síla na něj byla nulová, takže čistý tlak vyvážil váhu. Nyní zvažte stabilně se pohybující tekutinu. Je užitečné vizualizovat tok kreslením v proudnicích, čarách tak, že jejich směr je směr, kterým se tekutina pohybuje v každém bodě.

Tato zjednodušení vám ve skutečnosti nejen řeknou, jakým směrem se tekutina pohybuje, ale také poskytují určitou představu o rychlosti – tam, kde se blíží k sobě, se tekutina musí pohybovat rychleji, protože protéká stejné množství tekutiny přes užší region. Představte si nyní vzduchový válec pohybující se podél potrubí, jeho osa je rovnoběžná s proudnicí. Je zřejmé, že se musí zrychlovat, když vstupuje do úzké části trubice – protože úzkou částí protéká stejné množství vzduchu jako široká část, musí jít rychleji.

Ale pokud je malá válec kapaliny zrychluje, musí na něj působit síla, která ho tlačí zezadu.

Jeho váha zde není relevantní, protože se pohybuje vodorovně. Jedinou silou, která na něj působí, je tedy tlak a musíme dojít k závěru, že tlak v jeho zadní části je větší než tlak v jeho přední části. Při vstupu do úzké části proto musí tlak klesat. Abychom objasnili, o co jde, nakreslíme poměrně velký válec:

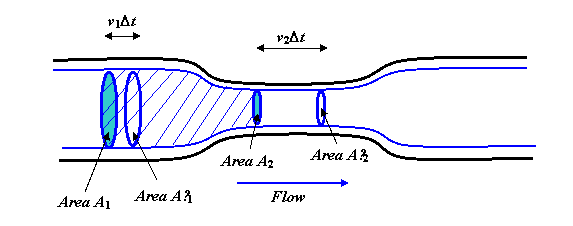
Tekutina plynule a plynule protéká potrubí. Silné modré čáry jsou proudnice, ve skutečnosti byste si měli představit otáčení celého diagramu kolem středové osy, abyste získali trojrozměrný obraz, a z modrých čar by se stal válec s užší částí „krku“, odrážející tvar potrubí.

Nyní vezměte v úvahu těleso kapaliny v uvedených proudnicích a na obou koncích jej uzavřete kruhovými oblastmi A1 a A2. Rychlost proudění kapaliny přes A1 musí být stejná jako rychlost protékat přes A2, protože při ustáleném průtoku se kapalina nemůže hromadit uprostřed (ani se odtud vyčerpávat). Objem protékající A1 během jedné sekundy je v1A1. (Chcete-li to vidět, představte si dlouhou rovnou trubku bez úzkého Pokud tekutina protéká řekněme 3 metry za sekundu, pak za jednu sekundu protéká veškerá tekutina, která byla ve vzdálenosti 3 metrů od oblasti A1 na straně proti proudu.)

Takže, tok přes A1 se rovná toku přes A2, \

(Poznámka pod čarou: Možná stojí za zmínku, že implicitně předpokládáme veloci ty je stejný ve všech bodech oblasti A1. Jakákoli skutečná tekutina má určitou viskozitu (tření) a bude se pohybovat pomaleji po stranách trubky než uprostřed. Budeme o tom diskutovat později. Prozatím považujeme „ideální“ tekutinu, což je termín používaný při ignorování viskozity. Výsledek, který odvodíme, je ve skutečnosti v pořádku – mohli jsme vzít malou oblast A1 daleko od stran, takže rychlost by byla stejné pro celou oblast, ale to by poskytlo mnohem méně jasný diagram.)

Nyní jsme připraveni zkoumat nárůst kinetické energie tekutiny, jak se zrychluje do úzké části, a pochopit, jak tlakový rozdíl odvedl práci nezbytnou k jeho urychlení.

\

Jediným možným zdrojem pro toto zvýšení energie je práce prováděná tlakem při tlačení tekutiny do úzká část.

\

Takže toto je práce na našem kusu tekutiny tím, že jej tekutina tlačí zezadu – ale to není konec příběhu, protože náš kus tekutina sama funguje a tlačí tekutinu před sebe, takže abychom zjistili celkový nárůst energie našeho bloku, musíme odečíst vnější práci, kterou dělá.To znamená, že celková práce vykonaná tlakem na naši tekutinu si

\

to pamatuje \ (A_1v_1 = A_2v_2 \).

Tato práce se musí rovnat změna kinetické energie, takže

\

z toho

\

Toto je Bernoulliho rovnice.

\.