A sum è il risultato di unaddizione. Ad esempio, aggiungendo 1, 2, 3 e 4 si ottiene la somma 10, scritta
 |
(1)
|
I numeri che vengono sommati sono chiamati addendi, o talvolta addendi. Loperazione di somma può essere indicata anche utilizzando un sigma maiuscolo con i limiti superiore e inferiore scritti sopra e sotto, e lindice sotto indicato. Ad esempio, la somma sopra potrebbe essere scritta
 |
(2)
|
Il la somma di un elenco di numeri viene implementata come Totale.
Una somma
 |
(3)
|
in cui ogni termine 
è dato da una regola fissa (ad esempio, 
è un pozzo -defined sequenza) è chiamata serie (finita), e se il numero di termini 
è infinito, la somma è chiamata serie infinita (o spesso solo “serie”). Una somma del modulo
 |
(4)
|
è chiamata serie geometrica .
Le condizioni per la convergenza di una serie possono essere determinate nel linguaggio Wolfram utilizzando SumConvergence.
La somma delle potenze finite generali
 |
(5)
|
può essere dato dallespressione
 |
(6)
|
che è equivalente alla formula di Faulhaber, dove la notazione 
indica la quantità in la domanda viene sollevata alla potenza appropriata 
e tutti i termini nella forma 
vengono sostituiti con il corrispondente I numeri di Bernoulli 
.
Unidentità divertente dovuta a J. Ziegenbein (pers. comm., 19 giugno 2002) deriva dallidentità
 |
(7)
|
che può essere scritto
 |
(8)
|
Pertanto, 
, ad esempio, può essere scritto nelle forme equivalenti
 |
 |
 |
(9)
|
 |
 |
 |
(10)
|
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
e così via.
Il teorema di Nicomaco fornisce come curiosa espressione la somma di potenza 
.
Le somme speciali includono
 |
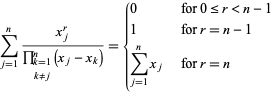(13)
|
e
 |
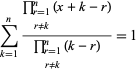(14)
|
Per ridurre al minimo la somma di un insieme di quadrati di numeri 
su un dato numero 
 |
 |
 |
(15 )
|
 |
 |
 |
(16)
|
prendi la derivata.
 |
(17)
|
Risolvendo per 
si ottiene
 |
(18)
|
quindi 
è ridotto a icona quando 
è impostato su significa.