Wprowadzenie do k-Nearest Neighbors: potężny algorytm uczenia maszynowego (z implementacją w Pythonie i R)

Uwaga: ten artykuł został pierwotnie opublikowany 10 października 2014 r. I zaktualizowany na 27 marca 2018 r.

Omówienie

• Poznaj k najbliższego sąsiada (KNN) – jeden z najpopularniejszych algorytmów uczenia maszynowego
• Poznaj działanie kNN w pythonie
• Wybierz odpowiednią wartość k w prostych słowach

Wprowadzenie

W ciągu czterech lat mojej kariery w dziedzinie data science zbudowałem ponad 80% modeli klasyfikacyjnych i tylko 15–20% modeli regresji. Te wskaźniki mogą być mniej lub bardziej uogólnione w całej branży. Przyczyną tego nastawienia w kierunku modeli klasyfikacyjnych jest to, że większość problemów analitycznych wiąże się z podjęciem decyzji.

Na przykład, czy klient będzie odstawał, czy nie, czy powinniśmy kierować do klienta X kampanie cyfrowe, niezależnie od tego, czy klient ma duży potencjał, itp. Te analizy są bardziej wnikliwe i bezpośrednio powiązane z planem wdrożenia.

W tym artykule omówimy inną szeroko stosowaną technikę klasyfikacji systemów uczących się, zwaną K-najbliższymi sąsiadami (KNN). Skupimy się przede wszystkim na tym, jak działa algorytm i jak parametr wejściowy wpływa na wynik / prognozę.

Uwaga: osoby, które wolą uczyć się za pomocą filmów, mogą się tego samego nauczyć podczas naszego bezpłatnego kursu – K- Algorytm najbliższych sąsiadów (KNN) w Pythonie i R. A jeśli jesteś zupełnie początkującym w nauce o danych i uczeniu maszynowym, sprawdź nasz program Certified BlackBelt –

• Certyfikowana sztuczna inteligencja & ML Blackbelt + Program

Spis treści

• Kiedy używamy algorytmu KNN?
• W jaki sposób Algorytm KNN działa?
• Jak dobieramy współczynnik K?
• Breaking it Down – pseudokod KNN
• Implementacja w Pythonie od zera
• Porównanie naszego modelu ze scikit-learn

Kiedy używamy algorytmu KNN?

KNN może być używany do obu klasyfikacja i regresja problemy predykcyjne. Jednak jest on szerzej stosowany w problemach klasyfikacyjnych w przemyśle. Aby ocenić jakąkolwiek technikę, zazwyczaj bierzemy pod uwagę 3 ważne aspekty:

1. Łatwość interpretacji wyników

2. Czas obliczeń

3. Moc predykcyjna

Weźmy kilka przykładów, aby umieścić KNN na skali:

Algorytm KNN sprawdza się we wszystkich parametrach rozważań. Jest powszechnie używany ze względu na łatwość interpretacji i krótki czas obliczeń.

Jak działa algorytm KNN?

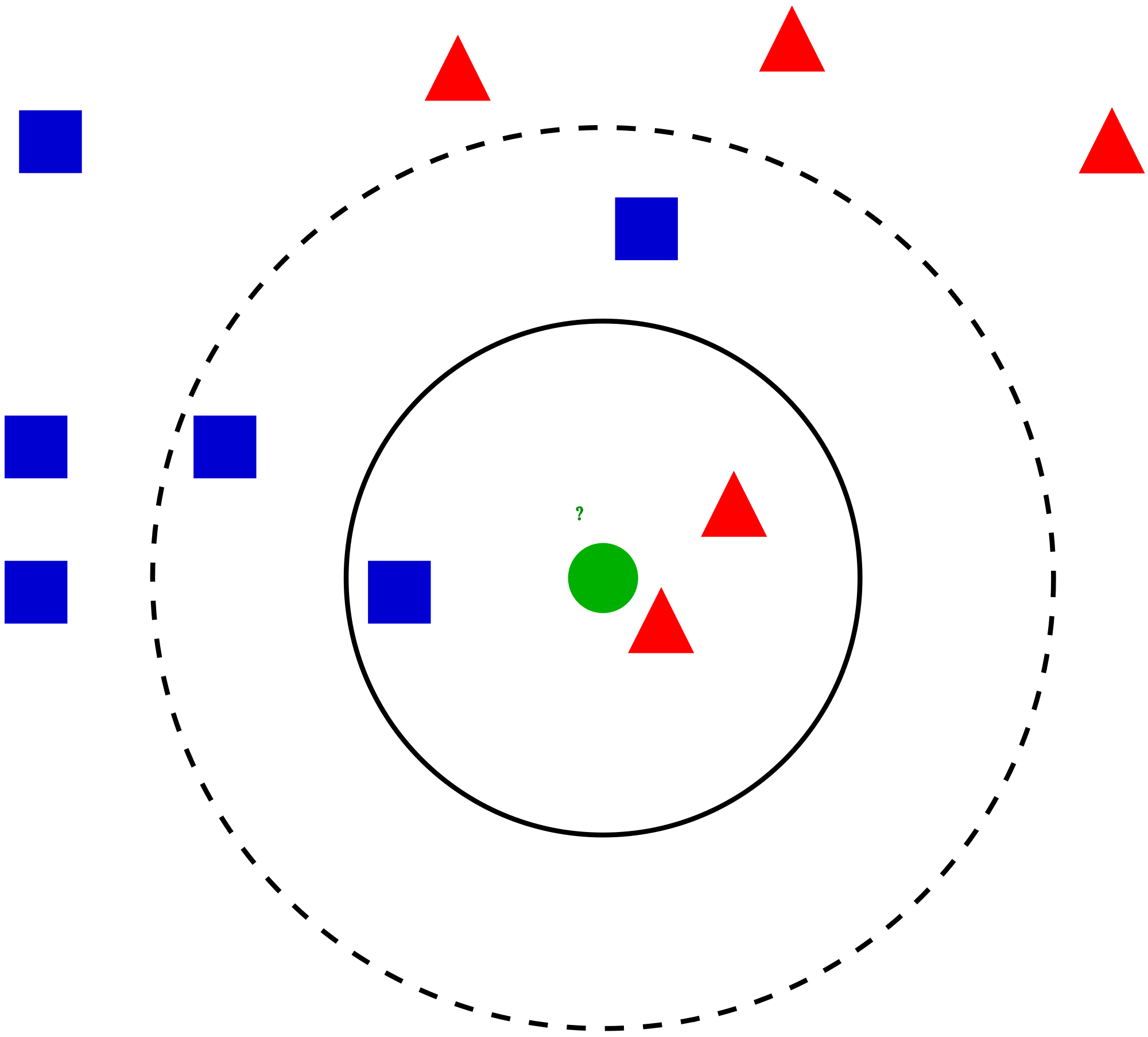
Rozważmy prosty przypadek zrozumieć ten algorytm. Poniżej znajduje się szereg czerwonych kółek (RC) i zielonych kwadratów (GS):

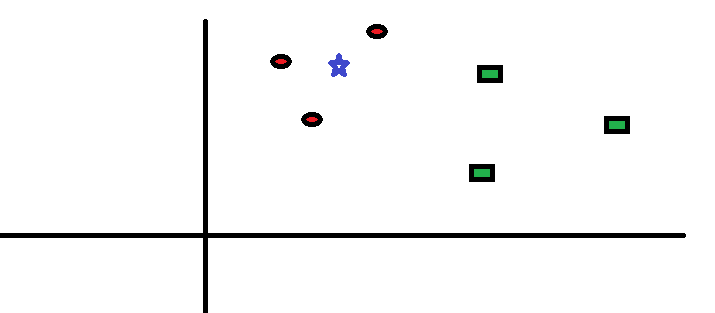Chcesz się dowiedzieć klasa niebieskiej gwiazdy (BS). BS może być RC lub GS i niczym więcej. Algorytm „K” to KNN jest najbliższym sąsiadem, od którego chcemy głosować. Powiedzmy, że K = 3. W związku z tym utworzymy teraz okrąg z BS jako środkiem tak dużym, aby obejmował tylko trzy punkty danych na płaszczyźnie . Aby uzyskać więcej informacji, zapoznaj się z poniższym diagramem:

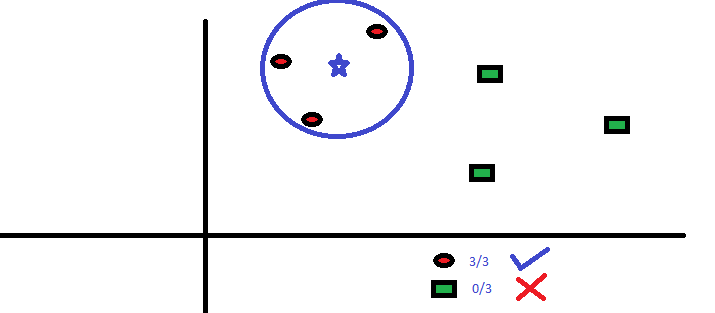Wszystkie trzy punkty najbliższe BS to RC. przy dobrym poziomie ufności możemy powiedzieć, że BS powinno należeć do klasy RC. Tutaj wybór stał się bardzo oczywisty, ponieważ wszystkie trzy głosy od najbliższego sąsiada trafiły do RC. Wybór parametru K jest bardzo istotny w tym algorytmie . Następnie zrozumiemy, jakie czynniki należy wziąć pod uwagę, aby uzyskać najlepszy K.

Jak wybrać współczynnik K?

Najpierw spróbujmy zrozumieć, na co dokładnie wpływa K. Jeśli widzimy ostatni przykład, zakładając, że wszystkie 6 obserwacji treningowych pozostają stałe, przy danej wartości K możemy wyznaczyć granice każdej klasy. te granice oddzielą RC od GS. W ten sam sposób spróbujmy zobaczyć wpływ wartości „K” na granice klas. Poniżej przedstawiono różne granice oddzielające dwie klasy o różnych wartościach K.

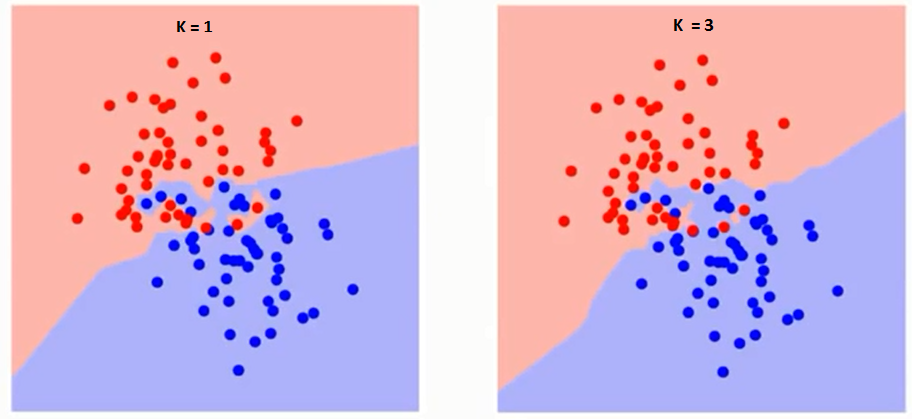
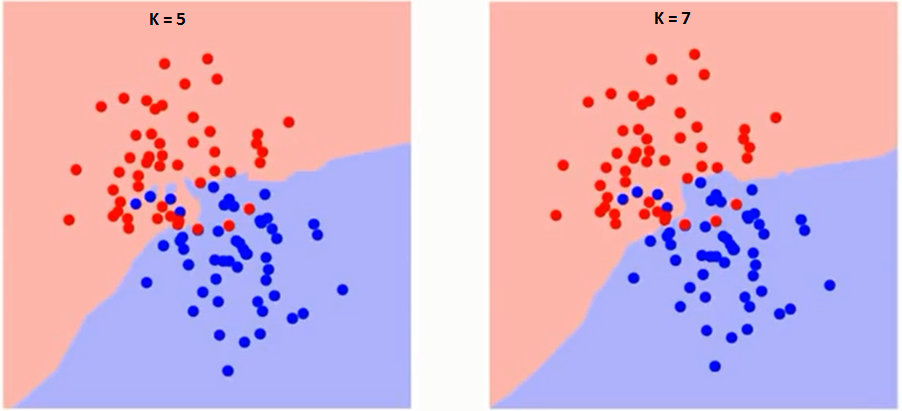
Jeśli przyjrzysz się uważnie, zobaczysz, że granica staje się gładsza wraz ze wzrostem wartości K. Wraz ze wzrostem K do nieskończoności ostatecznie staje się całkowicie niebieskie lub całkowicie czerwone, w zależności od całkowitej większości. Stopień błędów uczenia i współczynnik błędów walidacji to dwa parametry, których potrzebujemy, aby uzyskać dostęp do różnych wartości K. Poniżej znajduje się krzywa wskaźnika błędów uczenia ze zmienną wartością K:

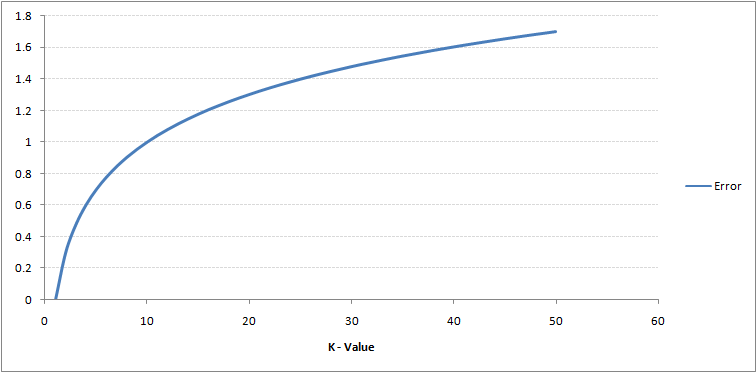Jak widać, współczynnik błędów przy K = 1 wynosi zawsze zero dla próbki uczącej.Dzieje się tak, ponieważ najbliższym punktem danych treningowych jest on sam, stąd prognoza jest zawsze dokładna przy K = 1. Jeśli krzywa błędu walidacji byłaby podobna, nasz wybór K byłby 1. Poniżej znajduje się krzywa błędu walidacji o zmiennej wartości K:

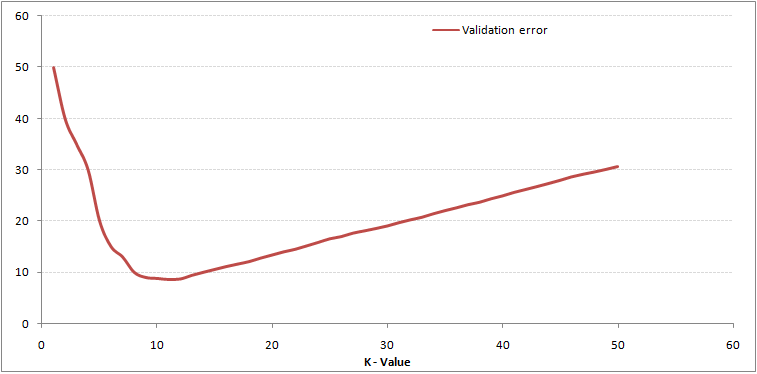To czyni historię bardziej przejrzystą. Przy K = 1 przekroczyliśmy granice. Stąd poziom błędu początkowo spada i osiąga minimum. Po osiągnięciu punktu minimalnego zwiększa się wraz ze wzrostem K. Aby uzyskać optymalną wartość K, można oddzielić szkolenie i walidację od początkowego zbioru danych. Teraz wykreśl krzywą błędu walidacji, aby uzyskać optymalną wartość K. Tę wartość K należy stosować do wszystkich prognoz.

Powyższą treść można zrozumieć bardziej intuicyjnie, korzystając z naszego swobodnego kursu – K-Nearest Neighbors ( KNN) Algorytm w Pythonie i R

Breaking it Down – pseudo Code of KNN

Możemy zaimplementować model KNN, wykonując poniższe kroki:

1. Załaduj dane
2. Zainicjuj wartość k
3. Aby uzyskać przewidywaną klasę, wykonaj iterację od 1 do całkowitej liczby punktów danych szkoleniowych
   1. Oblicz odległość między testami dane i każdy wiersz danych szkoleniowych. Tutaj użyjemy odległości euklidesowej jako metryki odległości, ponieważ jest to najpopularniejsza metoda. Inne metryki, których można użyć, to Czebyszewa, cosinus itp.
   2. Sortuj obliczone odległości w porządku rosnącym na podstawie wartości odległości
   3. Pobierz k górnych wierszy z posortowanej tablicy
   4. Pobierz najczęstszą klasę tych wierszy
   5. Zwróć przewidywaną klasę

Implementacja w Pythonie od podstaw

Będziemy używać popularnego zbioru danych Iris do budowy naszego modelu KNN. Możesz go pobrać stąd.

Porównanie naszego modelu ze scikit-learn

Widzimy, że oba modele przewidywały tę samą klasę (Iris- virginica ) i tych samych najbliższych sąsiadów (). Stąd możemy stwierdzić, że nasz model działa zgodnie z oczekiwaniami.

Implementacja kNN w R

Krok 1: Importowanie danych

Krok 2: Sprawdzanie danych i obliczanie podsumowania danych

Dane wyjściowe

Krok 3: Dzielenie danych

Krok 4: Obliczanie odległość euklidesowa

Krok 5: Zapis funkcji przewidującej kNN

Krok 6: Obliczanie etykiety (nazwy) dla K = 1

Dane wyjściowe

For K=1 "Iris-virginica"

W ten sam sposób możesz obliczyć inne wartości K.

Porównanie naszej funkcji predykcyjnej kNN z biblioteką „Class”

Dane wyjściowe

For K=1 "Iris-virginica"

Widzimy, że oba modele przewidywały tę samą klasę („Iris-virginica”).

Uwagi końcowe

Algorytm KNN jest jednym z najprostszych algorytmów klasyfikacji. Taka prostota może dawać wysoce konkurencyjne wyniki.Algorytm KNN może być również używany do problemów regresji. Jedyna różnica z omawianej metodologii będzie raczej wykorzystywanie średnich z najbliższych sąsiadów, a nie głosowań z najbliższych sąsiadów. KNN można zakodować w jednej linii w R. Jeszcze nie zbadałem, jak możemy użyć algorytmu KNN w SAS.

Czy artykuł był przydatny? Czy korzystałeś ostatnio z innego narzędzia do uczenia maszynowego? Czy planujesz wykorzystać KNN w którymkolwiek ze swoich problemów biznesowych? Jeśli tak, powiedz nam, jak planujesz to zrobić.

Jeśli podoba Ci się to, co właśnie przeczytałeś, & chcesz kontynuować naukę na temat analityki, zapisz się do naszego e-maile, śledź nas na Twitterze lub polub naszą stronę na Facebooku.