![]()
A suma jest wynikiem dodania. Na przykład dodanie 1, 2, 3 i 4 daje sumę 10 zapisaną
| |
(1)
|
Sumowane liczby nazywane są sumami lub czasami sumami. Operację sumowania można również wskazać za pomocą sigmy wielkiej z górną i dolną granicą zapisaną powyżej i poniżej oraz indeksem wskazanym poniżej. Na przykład powyższą sumę można zapisać
| |
(2)
|
suma listy liczb jest zaimplementowana jako Suma.
Suma
| |
(3)
|
, w którym każdy termin ![]() jest określony przez jakąś ustaloną regułę (tj.
jest określony przez jakąś ustaloną regułę (tj. ![]() to dobrze -definiowana sekwencja) nazywana jest (skończonym) szeregiem, a jeśli liczba wyrazów
to dobrze -definiowana sekwencja) nazywana jest (skończonym) szeregiem, a jeśli liczba wyrazów ![]() jest nieskończona, suma nazywana jest nieskończonym szeregiem (lub często po prostu „serią”). Suma postaci
jest nieskończona, suma nazywana jest nieskończonym szeregiem (lub często po prostu „serią”). Suma postaci
| |
nazywa się serią geometryczną .
Warunki zbieżności szeregu można określić w języku Wolfram za pomocą SumConvergence.
Ogólna suma potęg skończonych
| |
(5)
|
można podać za pomocą wyrażenia
| |
(6)
|
co jest odpowiednikiem formuły Faulhabera, gdzie zapis ![]() oznacza ilość w pytanie jest podnoszone do odpowiedniej potęgi
oznacza ilość w pytanie jest podnoszone do odpowiedniej potęgi ![]() , a wszystkie wyrazy w postaci
, a wszystkie wyrazy w postaci ![]() są zastępowane odpowiednim Liczby Bernoulliego
są zastępowane odpowiednim Liczby Bernoulliego ![]() .
.
Zabawna tożsamość autorstwa J. Ziegenbeina (pers. comm., 19 czerwca 2002) wynika z tożsamości
| |
(7)
|
które można zapisać
| |
(8)
|
Dlatego ![]() można zapisać w równoważnych formach
można zapisać w równoważnych formach
| |
|
|
(9)
|
| |
|
|
(10)
|
| |
|
|
(11)
|
| |
|
|
(12)
|
i tak dalej.
Twierdzenie Nicomachusa daje ciekawe wyrażenie na sumę potęg ![]() .
.
Specjalne sumy obejmują
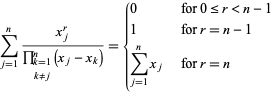 |
(13)
|
i
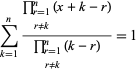 |
(14)
|
Aby zminimalizować sumę zestawu kwadratów liczb ![]() o danej liczbie
o danej liczbie ![]()
| |
|
|
(15 )
|
| |
|
|
(16)
|
weź pochodną.
| |
(17)
|
Rozwiązanie ![]() daje
daje
| |
(18)
|
więc ![]() jest zminimalizowane, gdy
jest zminimalizowane, gdy ![]() jest ustawiony na znaczy.
jest ustawiony na znaczy.