Jak zmienia się ciśnienie wraz ze zmianą objętości podczas adiabatycznej ekspansji i kompresji w idealnym gazie? Ta strona jest dodatkiem do naszej dyskusji na temat dźwięku. Powietrze pod ciśnieniem atmosferycznym jest gazem prawie idealnym, a transmisja dźwięku w powietrzu jest zbliżona do adiabatycznej dla normalnych częstotliwości i odległości transmisji. (Wrócimy do tego założenia poniżej.)
Pierwsza zasada termodynamiki wiąże zmianę energii wewnętrznej dU z pracą dW wykonaną przez system i dodanym do niego ciepłem dQ.
dU = dQ – dW
Z definicji, w procesie adiabatycznym, wymieniane ciepło dQ = 0. Zastępując to w pierwszym prawie i zmieniając układ, otrzymamy
0 = dQ = dU + dW
Drugi termin jest prosty: praca wykonana dW, gdy system zmienia swoją objętość V na dV, to PdV.
Pierwszy termin może odnosić się do ciepła właściwego, które jest definiowane jako ciepło dodane na jednostkę zmiany temperatury na mol substancji. Jeśli dodamy ciepło przy stałej objętości, gaz nie rozszerzy się i nie będzie działał. Zatem dodatkowe ciepło zwiększa energię wewnętrzną U. Zatem wynika z tej definicji, że ciepło właściwe przy stałej objętości wynosi ![]() , gdzie n to liczba moli. Stąd
, gdzie n to liczba moli. Stąd
Teraz równanie stanu gazu doskonałego to
nRT = PV ( ii)
gdzie R jest stałą gazową. Biorąc pochodne, otrzymujemy
Możemy teraz łączyć równania (i) i (iii), aby wyeliminować T. (i) oraz (ii) podaj odpowiednio następujące wyrażenia dla ncv dT:
Po zebraniu warunków PdV i VdP otrzymujemy
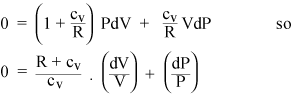
Jeśli gaz jest idealny, jego energia wewnętrzna jest w całości kinetyczna, więc energia wewnętrzna U zależy tylko od T. Z równania stanu gazu doskonałego (ii) możemy obliczyć praca dW wykonywana przy stałym ciśnieniu: to po prostu PdV = nRdT. Tak więc, jeśli dodamy ciepło do gazu przy stałym ciśnieniu, musimy podgrzać RdT dla każdego mola gazu, poza ciepłem, które powinniśmy dodać przy stałej objętości. Zatem ciepło właściwe gazu doskonałego przy stałym ciśnieniu wynosi zaledwie cP = cv + R. Stosunek ciepła określonego jest oznaczony standardowym symbolem:
. Mamy więc
(iv)
To jest główny wynik, który musimy omówić z falami dźwiękowymi: właśnie pokazaliśmy, że proporcjonalna zmiana ciśnienia jest – γ razy większa od proporcjonalnej zmiany objętości lub γ razy proporcjonalna do zmiany gęstości.
Nie poprzestawajmy jednak na tym, ponieważ jesteśmy tylko kilka linii od ważnego wyniku. Wiemy, że d (ln x) = dx / x (dowód w rachunku różniczkowym). Możemy więc napisać poprzednie równanie jako
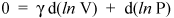
i przeorganizuj go, aby uzyskać
(v)
Dlatego w przypadku procesu adiabatycznego w gazie idealnym
. (vi)
Po rozważeniu zgadzasz się, że cP > cV: At stała objętość, wszystko co Ciepło, które wprowadzasz, zwiększa energię wewnętrzną, a tym samym podnosi temperaturę. Przy stałym ciśnieniu należy wkładać nie tylko ciepło, które podnosi energię wewnętrzną, ale także ilość ciepła równą pracy wykonanej podczas rozszerzalności cieplnej układu. Dla powietrza γ wynosi około 1,4.
Oczywiście możemy teraz podstawić do (vi) z równania stanu (ii), aby zobaczyć, jak P i T lub T i V są powiązane z procesem adiabatycznym.
Kiedy dźwięk jest adiabatyczny?
Wspomnieliśmy powyżej, że „transmisja dźwięku w powietrzu jest zbliżona do adiabatycznej dla normalnych częstotliwości i odległości transmisji”. Kiedy to się nie udaje? Przy maksimach ciśnienia fali dźwiękowej temperatura jest wysoka. Spodziewamy się więc, że część ciepła rozproszy się do sąsiednich minimów ciśnienia. Oczywiście w ciągu pół okresu fali dźwiękowej nie ma dużo czasu na rozproszenie ciepła przez połowę długości fali. Jednak czas potrzebny na rozproszenie ciepła jest kwadratem odległości. Tak więc proces ten jest mniej pomijalny dla wysokich częstotliwości, ponieważ krótsza połowa długości fali więcej niż kompensuje krótszy półokres. Ta dyfuzja usuwa energię mechaniczną z fali, szczególnie przy wysokich częstotliwościach, a efekt zwiększa się wraz z odległością transmisji.Z tego powodu (a czasem i innych) odległe dźwięki są nie tylko mniej głośne, ale także mniej jasne niż bliskie.