Poniżej znajdują się kalkulatory do obliczenia powierzchni siedmiu typowych kształtów. Obszar bardziej złożonych kształtów można zwykle uzyskać przez rozbicie ich na ich proste, zagregowane kształty i zsumowanie ich powierzchni. Ten kalkulator jest szczególnie przydatny do szacowania powierzchni terenu.

Prostokąt
Trójkąt
Użyj kalkulatora trójkąta, aby określić
wszystkie trzy krawędzie trójkąta
podając inne parametry.
Trapez
Okrąg

Sektor

Elipsa
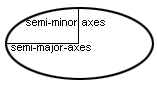
Równoległobok
Kalkulator powierzchni pokrewnych | Kalkulator objętości
Powierzchnia to wielkość opisująca rozmiar lub zakres dwuwymiarowej figury lub kształtu na płaszczyźnie. Można to wizualizować jako ilość farby, jaka byłaby potrzebna do pokrycia powierzchni i jest to dwuwymiarowy odpowiednik jednowymiarowej długości krzywej i trójwymiarowej objętości ciała stałego. Standardową jednostką powierzchni w międzynarodowym układzie jednostek SI jest metr kwadratowy lub m2. Poniżej przedstawiono równania dla niektórych z najczęstszych prostych kształtów oraz przykłady obliczania pola powierzchni każdego z nich.
Prostokąt
Prostokąt to czworokąt z czterema kątami prostymi. Jest to jeden z najprostszych kształtów, a obliczenie jego powierzchni wymaga jedynie znajomości (lub możliwości zmierzenia) jego długości i szerokości. Czworokąt z definicji to wielokąt, który ma cztery krawędzie i wierzchołki. W przypadku prostokąta długość zwykle odnosi się do dwóch dłuższych krawędzi czworoboku, podczas gdy szerokość odnosi się do krótszej z dwóch krawędzi. Gdy długość i szerokość prostokąta są równe, kształt jest specjalnym przypadkiem prostokąta, zwanym kwadratem. Równanie do obliczenia pola prostokąta jest następujące:
powierzchnia = długość × szerokość
Rolnik i jego córka – niesprzedana ziemia
Wyobraź sobie rolnika próbując sprzedać kawałek ziemi, który okazał się być idealnie prostokątny. Ponieważ ma kilka krów, których nie chciał swobodnie bawić się, ogrodził kawałek ziemi i zna dokładną długość i szerokość każdej krawędzi. Rolnik mieszka również w Stanach Zjednoczonych i nie jest zaznajomiony z używaniem jednostek SI, nadal mierzy swoją działkę w stopach. Stopa została określona na dokładnie 0,3048 metra w 1959 roku po jej zmianie przez długi okres czasu, ponieważ historycznie, ciało ludzkie było często używane jako podstawa dla jednostek długości i, co nie dziwi, było niespójne pod względem czasu i lokalizacji. Stycznie na bok, działka rolnika ma długość 220 stóp i szerokość 99 stóp. Korzystając z tych informacji:
powierzchnia = 220 × 99 = 21780 stóp kwadratowych
Działka rolnika, która ma powierzchnię 21 780 stóp kwadratowych, odpowiada pół akra, gdzie akr jest zdefiniowany jako obszar 1 łańcucha na 1 furlong, który jest określony przez coś innego i tak dalej, i dlatego SI teraz istnieje. Na nieszczęście dla rolnika mieszka na obszarze zdominowanym przez zagranicznych inwestorów o mniejszych stopach, którzy uważali, że powinni dostać więcej metrów kwadratowych za swoje pieniądze, a jego ziemia pozostaje niesprzedana do dziś.
Trójkąt
Istnieje wiele równań służących do obliczania pola powierzchni trójkąta na podstawie dostępnych informacji. Jak wspomniano w powyższym kalkulatorze, użyj kalkulatora trójkąta, aby uzyskać dalsze szczegóły i równania do obliczania pola powierzchni trójkąta, a także do określania boków trójkąta przy użyciu wszelkich dostępnych informacji. Krótko mówiąc, równanie użyte w powyższym kalkulatorze jest znane jako wzór Herona (czasami nazywany formułą Bohatera), odnosząc się do Bohatera Aleksandrii, greckiego matematyka i inżyniera, uważanego przez niektórych za największego eksperymentatora starożytności. Wzór jest następujący:

Rolnik i jego córka – oszołomienie trójkątem
W tym momencie z czasem, dzięki ogromnemu wysiłkowi i wytrwałości, rolnik w końcu sprzedał swoją działkę o powierzchni 21 780 stóp kwadratowych i postanowił przeznaczyć część zarobionych pieniędzy na budowę basenu dla swojej rodziny. Na nieszczęście dla rolnika nie bierze pod uwagę faktu, że koszty utrzymania basenu tylko przez jeden rok mogłyby prawdopodobnie opłacić jego dzieci odwiedzanie dowolnego basenu lub parku wodnego w nadchodzących latach.Jeszcze bardziej niefortunnie dla rolnika, jego 7-letnia córka, która niedawno podróżowała do Egiptu zastępczo przez Dorę the Explorer, zakochała się w trójkątach i nalega, aby basen był nie tylko trójkątny, ale także aby pomiary musi zawierać tylko cyfrę 7, aby reprezentować jej wiek i uwiecznić ten punkt jej życia w postaci trójkątnego basenu. Będąc kochającym ojcem, rolnik zgadza się na prośbę córki i przystępuje do planowania budowy swojego trójkątnego basenu. Rolnik musi teraz ustalić, czy na swoim podwórku ma wystarczającą powierzchnię, aby pomieścić basen. Podczas gdy rolnik zaczął się uczyć więcej o jednostkach SI, na razie nie czuje się komfortowo z ich użyciem i decyduje, że jego jedyną realną opcją jest zbudowanie basenu w postaci trójkąta równobocznego o bokach 77 stóp długości, ponieważ każda inna odmiana byłaby albo za duża, albo za mała . Biorąc pod uwagę te wymiary, rolnik określa niezbędny obszar w następujący sposób:

Ponieważ największa odległość między dwoma dowolnymi punktami trójkąt równoboczny to długość krawędzi trójkąta, rolnik rezerwuje krawędzie basenu do pływania „okrążeń” w swoim trójkątnym basenie o maksymalnej długości około połowy długości basenu olimpijskiego, ale o podwójnej powierzchni – wszystko pod czujne oczy przewodniczącej basenu, h jest córką i potępiającym spojrzeniem jego żony.
Trapez
Trapez to prosty wypukły czworokąt, który ma co najmniej jedną parę równoległych boków. Właściwość wypukłości oznacza, że kąt trapezu nie przekracza 180 ° (w przeciwieństwie do wklęsłego czworoboku), podczas gdy prostota oznacza, że trapezoidy nie przecinają się same, co oznacza, że dwa nieprzylegające boki nie przecinają się. trapezoid, równoległe boki nazywane są podstawami trapezu, a pozostałe dwa boki nazywane są nogami. Istnieje więcej rozróżnień i klasyfikacji dla różnych typów trapezów, ale ich powierzchnie są nadal obliczane w ten sam sposób przy użyciu następujące równanie:
| area = |
b1 + b2
|
× h |
Rolnik i jego córka – Ramping Endeavors
Minęły dwa lata od basen rolnika został ukończony, a jego córka urosła i dojrzała. Podczas gdy jej miłość do trójkątów wciąż trwa, w końcu doszła do wniosku, że bez względu na to, jak bardzo była „potrójna”, same trójkąty nie są w stanie wprawić świata w ruch, a warsztat Świętego Mikołaja nie może wiarygodnie balansować na biegunie północnym, były światem raczej piramidą niż kulą. Powoli zaczęła akceptować inne kształty w swoim życiu i realizuje niezliczone zainteresowania – obecnie freestyle BMX. W związku z tym potrzebuje rampy, ale niestety dla rolnika, nie byle jaka Rampa musi składać się tylko z kształtów, które można uformować za pomocą wielu trójkątów, ponieważ córka farmera, podobnie jak jej rap idolka BoB, nadal ma trudności z zaakceptowaniem rzeczywistości zakrzywionych powierzchni. Musi oczywiście używać tylko cyfry 9 w swoich pomiarach, aby odzwierciedlić jej wiek. Rolnik decyduje, że jego najlepszą opcją jest zbudowanie rampy złożonej z wielu prostokątów, z boczną ścianą rampy w kształcie trapezu. Ponieważ rolnik poczuł się teraz bardziej komfortowo z SI, może być bardziej kreatywny w używaniu jednostek i może zbudować rampę o bardziej rozsądnych rozmiarach, spełniając wymagania córki. Decyduje się zbudować rampę z trapezem ściana o wysokości 9 stóp, dolna podstawa o długości 29,528 stóp (9 m) i górna podstawa o 9 stóp. Powierzchnia trapezu jest obliczana w następujący sposób:
| area = |
9 + 29,528
|
× 9 = 173,376 stopy kw. |
Okrąg
Okrąg to prosty zamknięty kształt utworzony przez zbiór wszystkich punktów na płaszczyźnie, które znajdują się w określonej odległości od danego punktu środkowego. Ta odległość od środka do dowolnego punktu na okręgu nazywa się promieniem. Więcej szczegółów można znaleźć w odniesieniu do okręgi na stronie Kalkulatora okręgów, ale aby obliczyć powierzchnię, wystarczy znać promień i zrozumieć, że wartości w okręgu są powiązane przez h stała matematyczna π. Równanie do obliczenia pola koła jest następujące:
area = πr2
Rolnik i jego córka – Circle of Li (f) es
Minęło kolejne sześć lat, a jego córka wyrosła na silnego, pięknego, potężnego, pewnego siebie 15-letniego niewdzięcznika, skupionego wyłącznie na szukaniu zewnętrznego potwierdzenia ze strony znajomych i nieznajomych w mediach społecznościowych, całkowicie ignorując autentyczne wsparcie ze strony najbliższej rodziny i przyjaciół.Po kłótni z ojcem na temat nadmiernego korzystania z mediów społecznościowych, postanawia żerować na jego lęku przed nieznanym i wiarą w zjawiska nadprzyrodzone, aby zrobić mu psikusa. Nie wiedząc od czego zacząć, chodzi po mieście rozmawia z różnymi nieznajomymi, z których wszyscy pozornie mają niekończące się źródła mądrości i porad, gdzie dowiaduje się o kręgach zbożowych i ich powiązaniach z kosmitami i niezidentyfikowanymi obiektami latającymi, a także wielu innych tematach, które ignorują wszelkie naukowe i logiczne wyjaśnienia. przekonana o kulistej naturze Ziemi, usunęła wszystkie swoje poprzednie posty w mediach społecznościowych dotyczące BoB i rozszerzyła swoją miłość do trójkątów na akceptację innych kształtów, postanawia stworzyć podstawowy krąg zbożowy składający się z wielu koncentrycznych okręgów i chce określić obszar potrzebny do utworzenia kręgu zbożowego o zewnętrznym promieniu 15 stóp. Robi to, korzystając z następującego równania:
area = π × 152 = 706,858 sq ft
Niefortunny dla rolnika nie tylko boi się kręgu zbożowego, który pojawił się w nocy w nocy, gdy jego córka powiedziała mu, że jest na piżamowej imprezie z przyjaciółmi, że z jakiegoś dziwnego powodu nie zaowocował zbędnymi postami na Instagramie (był oczywiście pierwszy naśladowca jego córki), ale liczba „kręgu śledczych” i „cereologów” pojawiających się na jego farmie w celu zbadania, a następnie potwierdzenia autentyczności kręgu zbożowego jako konstrukcji kosmitów, kosztowała go znaczne szkody dla jego uprawy.
Sektor
Sektor koła to w zasadzie część koła otoczona dwoma promieniami i łukiem. Biorąc pod uwagę promień i kąt, pole powierzchni sektora można obliczyć mnożąc powierzchnię całego koła przez stosunek znanego kąta do 360 ° lub 2π radianów, jak pokazano w poniższym równaniu:
| area = |
θ
|
× πr2 | jeśli θ jest w stopniach |
lub
| area = |
θ
|
× πr2 | jeśli θ to w radianach |
Rolnik i jego córka – rodzina podzielona na części
Rolnik i jego rodzina stoją przed najważniejszym dylemat do chwili obecnej. Minął rok, a córka rolnika ma już 16 lat i w ramach obchodów urodzin jej mama upiekła swój ulubiony deser, placek z jeżynami. Niestety dla córki rolnika, ciasto jeżynowe również przypadło do gustu pożywienie ich ulubionego szopa pracza, Dziobaka, o czym świadczy brak ciasta o wartości 180 ° z charakterystycznymi oznakami sprawcy w postaci okruchów prowadzących w kierunku nadmiernie pobłażliwego szopa pracza. Początkowo placek z łatwością zostałby podzielony między trzy osoby i jednego szopa, ale teraz połowę ciasta należy podzielić między trzy osoby, tak jak zmartwiony, ale nasycony dziobak obserwuje z daleka. Biorąc pod uwagę, że każda osoba otrzyma placek o wartości 60 ° o promieniu 16 cali, obszar ciasta, który każda osoba otrzymuje, można obliczyć w następujący sposób:
powierzchnia = 60 ° / 360 ° × π × 162 = 134.041 in2
W wyniku bezmyślności Dziobaka każda osoba dostaje o jedną trzecią mniej ciasta, a córka z rozmysłem przypomina amerykańskie lekcje historii, na których dowiedziała się o bitwie nad Alamo i przedstawieniu bohater ludowy Davy Crockett i jego czapka z szopowej skóry.
Elipsa
Elipsa jest uogólnioną formą koła i jest krzywą na płaszczyźnie, w której suma odległości punkt na krzywej do każdego z jej dwóch ogniskowych jest stały, jak pokazano na poniższym rysunku, gdzie P to dowolny punkt na elipsie, a F1 i F2 to dwa ogniska.
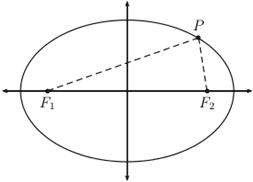
Gdy F1 = F2, wynikowa elipsa jest okręgiem. Półoś większa oś elipsy, jak pokazano na rysunku będącym częścią kalkulatora, to najdłuższy promień elipsy, whil e oś półosiowa jest najkrótsza. Główne i mniejsze osie odnoszą się do średnic, a nie do promieni elipsy. Równanie do obliczania pola elipsy jest podobne do równania do obliczania pola koła, z tą różnicą, że stosuje się dwa promienie zamiast jednego (ponieważ ogniska znajdują się w tym samym miejscu dla koła):
area = πab
gdzie aib to osie semi-major i semi-minor
Rolnik i jego córka – wypadają z orbity
Dwa Minęły lata od tajemniczego zaginięcia rodzinnego zwierzaka, Dziobaka i szczęśliwej wygranej w postaci futrzanego dodatku przez córkę farmera w szkolnej loterii, która pomogła wypełnić pustkę po stracie ich ukochanego zwierzaka. Córka rolnika ma teraz 18 lat i jest gotowa uciec z wiejskiej Montany, aby rozpocząć studia pełne wolności i rozpusty oraz oczywiście dodatkowej nauki.Na nieszczęście dla córki rolnika dorastała w środowisku pełnym pozytywnych wzmocnień, a co za tym idzie, mentalności, że należy „strzelać do księżyca, nawet jeśli tęsknisz,„ wylądujesz wśród gwiazd ”, a także zapewnienie ze strony wszystkich wokół niej, że może zrobić absolutnie wszystko, na co się zdecyduje! W związku z tym, z jej nieoptymalnymi ocenami, brakiem jakichkolwiek zajęć pozalekcyjnych z powodu niezliczonych różnych zainteresowań pochłaniających cały jej wolny czas, zerowego planowania i jej nalegania na składanie wniosków tylko na najlepszych z najlepszych uniwersytetów, szok, który wywołał, gdy ona nie została przyjęta na żaden z najlepszych uniwersytetów, na które złożyła podanie, można to rozsądnie porównać do jej metaforycznego lądowania w kosmosie, nadmuchiwania, zamrażania i szybkiego duszenia się, gdy przegapiła księżyc i wylądowała wśród gwiazd. Wraz z płucami jej marzenie o zostaniu astrofizykiem zostało przerwane, przynajmniej na razie, i została zdegradowana do obliczenia eliptycznego obszaru niezbędnego w jej pokoju do zbudowania prawie eliptycznej orbity Ziemi o wielkości człowieka. słońce, aby mogła tęsknie wpatrywać się w słońce pośrodku swojego pokoju i jego uosobienie jej serca, płonącego namiętnością, ale otoczonego zimnym bezkresem przestrzeni, z odległym obrotem Ziemi kpiąco przedstawiającym odległość między jej snami i solidne podłoże.
powierzchnia = π × 18 ft × 20 ft = 1130,97 sq ft
Równoległobok
Równoległobok to prosty czworobok, który ma dwie pary równoległych boków, gdzie przeciwległe boki i kąty czworoboku mają równe długości i kąty. Prostokąty, romby i kwadraty to szczególne przypadki równoległoboków. Pamiętaj, że klasyfikacja „prostego” kształtu oznacza, że kształt nie przecina się samodzielnie. Równoległobok można podzielić na trójkąt prostokątny i trapez, które można dalej przestawić, aby utworzyć prostokąt, dzięki czemu równanie do obliczenia pola powierzchni równoległoboku jest zasadniczo takie samo, jak w przypadku obliczenia prostokąta. Jednak zamiast długości i szerokości w równoległoboku używa się podstawy i wysokości, gdzie wysokość jest długością prostopadłej między parą podstaw. Na podstawie poniższego rysunku równanie do obliczania pola powierzchni równoległoboku wygląda następująco:
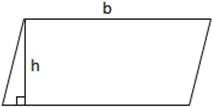
area = b × h
Rolnik i jego córka – diament na niebie
Minęły kolejne dwa lata w życiu rolnika i jego rodziny i chociaż jego córka była powodem do intensywnych zmartwień , w końcu pokonała dystans między płonącym słońcem, które jest jej sercem, a Ziemią, na której społeczeństwo upiera się, że musi pozostać ugruntowana. Dzięki zmaganiom, które wynikły z jej narzuconej sobie izolacji, otoczonej wyimaginowanymi, osądzającymi oczami, zakładającymi porażkę ze wszystkich stron, córka rolnika wyłoniła się z nacisków ziemi jak diament, lśniąc jasno i stanowczo w swoim postanowieniu. decyduje, że nie ma innego wyjścia, jak przetrwać na polu życia asteroid w nadziei, że istnieje bajkowe zakończenie Disneya. Nareszcie, na szczęście dla córki rolnika i jej rodziny, nadzieja się pojawia, ale nie w formie księcia z bajki, ale raczej jako znak z rzekomych niebios. Poprzez wszystkie jej metaforyczne rozważania i udręki związane z przestrzenią, staje się prawie wiarygodne, że córka rolnika w jakiś sposób wpłynęła na ogromną ośmiościenną diamentową asteroidę spadającą prosto, ale bezpiecznie na ich pola uprawne, co interpretuje jako reprezentujące jej podróż, formację i ostateczny powrót do domu . Córka rolnika przystępuje do pomiaru powierzchni jednej z romboidalnych powierzchni jej nowo odnalezionego symbolu życia:
powierzchnia = 20 stóp × 18 stóp = 360 stóp kwadratowych
Na nieszczęście dla córki rolnika, pojawienie się olbrzymiego diamentu zwróciło uwagę całego świata i po dostatecznym nacisku poddaje się w sobie człowiekowi i sprzedaje diament, będący odzwierciedleniem jej życia i duszy, zamożną kolekcjonerkę i spędza resztę życia w rozrzutnym pobłażaniu, porzucając swoje przekonania i zatracając się w czarnej dziurze społeczeństwa.