Algorytm Breadth First Search (BFS) z EXAMPLE

Co to jest algorytm BFS (przeszukiwanie wszerz)?

Przeszukiwanie wszerz (BFS) jest algorytmem używanym do tworzenia wykresów danych lub przeszukiwania drzew lub konstrukcji przechodzących. Pełna forma BFS to wyszukiwanie wszerz.

Algorytm skutecznie odwiedza i zaznacza wszystkie kluczowe węzły na wykresie w dokładny, szeroki sposób. Ten algorytm wybiera pojedynczy węzeł (punkt początkowy lub źródłowy) na wykresie, a następnie odwiedza wszystkie węzły sąsiadujące z wybranym węzłem. Pamiętaj, że BFS uzyskuje dostęp do tych węzłów jeden po drugim.

Gdy algorytm odwiedza i zaznacza węzeł początkowy, przesuwa się w kierunku najbliższych nieodwiedzonych węzłów i analizuje je. Po odwiedzeniu wszystkie węzły są zaznaczane. Te iteracje są kontynuowane, dopóki wszystkie węzły wykresu nie zostaną pomyślnie odwiedzone i oznaczone.

W tym samouczku dotyczącym algorytmu dowiesz się:

• Co to jest algorytm BFS (przeszukiwanie wszerz)?
• Co to jest przechodzenie wykresów?
• Architektura algorytmu BFS
• Dlaczego potrzebujemy algorytmu BFS?
• Jak działa algorytm BFS?
• Przykład algorytmu BFS
• Reguły algorytmu BFS
• Zastosowania algorytmu BFS

Co to jest przemierzanie wykresów?

Przechodzenie przez wykres to powszechnie stosowana metodologia lokalizowania położenia wierzchołka na wykresie. Jest to zaawansowany algorytm wyszukiwania, który potrafi szybko i precyzyjnie analizować wykres wraz z zaznaczaniem kolejności odwiedzanych wierzchołków. Ten proces umożliwia szybkie odwiedzanie każdego węzła na wykresie bez zamykania się w nieskończonej pętli.

Architektura algorytmu BFS

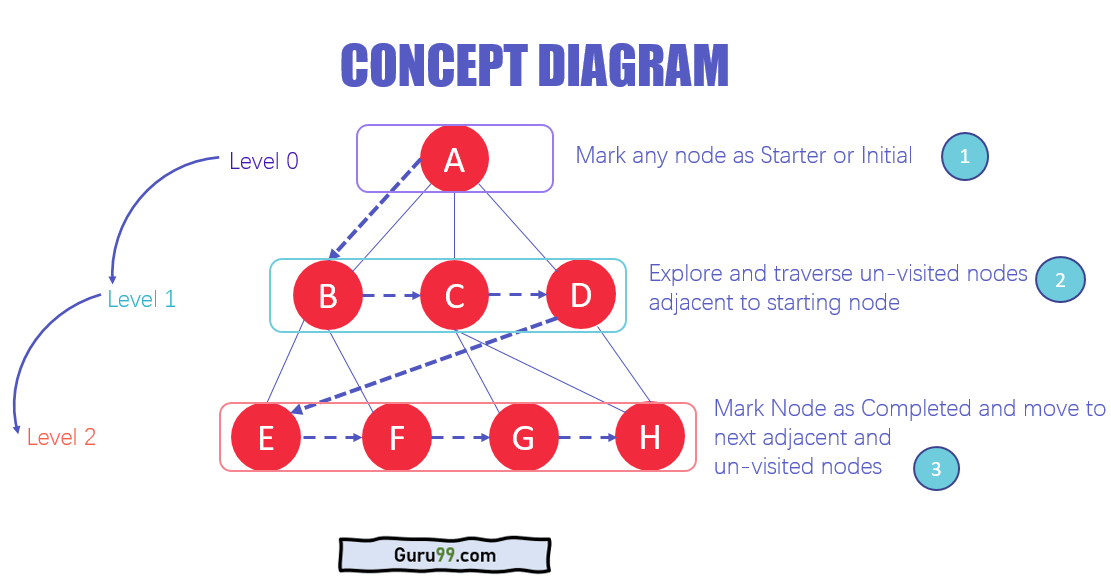
1. Na różnych poziomach danych możesz oznaczyć dowolny węzeł jako początkowy lub węzeł początkowy do rozpoczęcia przemierzania. BFS odwiedzi węzeł i oznaczy go jako odwiedzony i umieści go w kolejce.
2. Teraz BFS odwiedzi najbliższe i nieodwiedzone węzły i oznaczy je. Te wartości są również dodawane do kolejki. Kolejka działa w modelu FIFO.
3. W podobny sposób pozostałe najbliższe i nieodwiedzone węzły na wykresie są analizowane, zaznaczane i dodawane do kolejki. Te elementy są usuwane z kolejki w momencie odbioru i drukowane jako wynik.

Dlaczego potrzebujemy algorytmu BFS?

Istnieje wiele powodów, dla których warto wykorzystać algorytm BFS do wyszukiwania zbioru danych. Oto niektóre z najważniejszych aspektów, które sprawiają, że ten algorytm jest Twoim pierwszym wyborem:

• BFS jest przydatny do analizowania węzłów na wykresie i konstruowania najkrótszej ścieżki przechodzenia przez nie.
• BFS może przechodzić przez wykres w najmniejszej liczbie iteracji.
• Architektura algorytmu BFS jest prosta i solidna.
• Wynik algorytmu BFS zapewnia wysoki poziom dokładności w porównaniu z innymi algorytmami.
• Iteracje BFS są płynne i nie ma możliwości, aby ten algorytm został wciągnięty w problem nieskończonej pętli.

Jak działa algorytm BFS?

Przechodzenie przez wykres wymaga, aby algorytm odwiedzał, sprawdzał i / lub aktualizował każdy nieodwiedzony węzeł w strukturze drzewiastej. Przejścia przez wykres są klasyfikowane według kolejności, w jakiej odwiedzają węzły na wykresie.

Algorytm BFS rozpoczyna operację od pierwszego lub początkowego węzła na grafie i dokładnie ją przemierza. Po pomyślnym przejściu przez początkowy węzeł, następny nieprzekraczany wierzchołek na wykresie jest odwiedzany i oznaczany.

W związku z tym można powiedzieć, że wszystkie węzły przylegające do bieżącego wierzchołka są odwiedzane i przemierzane w pierwszej iteracji. Do implementacji algorytmu BFS stosowana jest prosta metodologia kolejkowania, która składa się z następujących kroków:

Krok 1)

Każdy wierzchołek lub węzeł na wykresie jest znany. Na przykład możesz oznaczyć węzeł jako V.

Krok 2)

W przypadku braku dostępu do wierzchołka V dodaj wierzchołek V do kolejki BFS

Krok 3)

Rozpocznij wyszukiwanie BFS i po zakończeniu zaznacz wierzchołek V jako odwiedzony.

Krok 4)

Kolejka BFS jest nadal nie jest pusty, stąd usuń wierzchołek V wykresu z kolejki.

Krok 5)

Pobierz wszystkie pozostałe wierzchołki na wykresie sąsiadującym z wierzchołkiem V

Krok 6)

Dla każdego sąsiedniego wierzchołka powiedzmy V1, jeśli nie jest jeszcze odwiedzany, dodaj V1 do kolejki BFS

Krok 7)

BFS odwiedzi wersję 1, oznaczy ją jako odwiedzoną i usunie z kolejki.

Przykład algorytmu BFS

Krok 1)

Masz wykres siedem liczb od 0 do 6.

Krok 2)

0 lub zero zostało oznaczone jako węzeł główny.

Krok 3)

0 jest odwiedzane, zaznaczane i wstawiane do struktury danych kolejki.

Krok 4)

Pozostałe 0 sąsiednich i nieodwiedzonych węzłów jest odwiedzanych, oznaczanych i wstawianych do kolejki.

Krok 5)

Iteracje przechodzenia są powtarzane, dopóki nie zostaną odwiedzone wszystkie węzły.

Reguły algorytmu BFS

Oto ważne zasady korzystania z algorytmu BFS:

• Kolejka (FIFO-First in First Out) Struktura danych jest używany przez BFS.
• Zaznaczasz dowolny węzeł na wykresie jako korzeń i zaczynasz przemierzać dane z niego.
• BFS przechodzi przez wszystkie węzły na wykresie i upuszcza je jako ukończone.
• BFS odwiedza sąsiedni nieodwiedzony węzeł, oznacza go jako ukończony i wstawia do kolejki.
• Usuwa poprzedni wierzchołek z kolejki w przypadku, gdy nie zostanie znaleziony sąsiedni wierzchołek.
• Algorytm BFS wykonuje iteracje, dopóki wszystkie wierzchołki grafu nie zostaną pomyślnie pokonane i oznaczone jako zakończone.
• Nie ma pętli spowodowanych przez BFS podczas przechodzenia przez dane z dowolnego węzła.

Zastosowania algorytmu BFS

Weźmy spójrz na niektóre z rzeczywistych aplikacji, w których implementacja algorytmu BFS może być bardzo skuteczna.

• Wykresy nieważone: algorytm BFS może łatwo utworzyć najkrótszą ścieżkę i minimalne drzewo rozpinające, aby odwiedzić wszystkie wierzchołki wykresu w jak najkrótszym czasie z dużą dokładnością.
• Sieci P2P: BFS można zaimplementować w celu zlokalizowania wszystkich najbliższych lub sąsiednich węzłów w sieci peer-to-peer. To przyspieszy znalezienie wymaganych danych .
• Przeszukiwacze sieci: wyszukiwarki lub roboty sieciowe mogą z łatwością budować wiele poziomów indeksów za pomocą BFS. Implementacja BFS rozpoczyna się od źródła, którym jest strona internetowa, a następnie odwiedza wszystkie linki z tego źródła. .
• Systemy nawigacji: BFS może pomóc znaleźć wszystkie sąsiednie lokalizacje z lokalizacji głównej lub źródłowej.
• Transmisja sieciowa ing: pakiet rozgłaszany jest kierowany przez algorytm BFS, aby znaleźć i dotrzeć do wszystkich węzłów, dla których ma adres.

Podsumowanie

• Przechodzenie przez wykres to unikalny proces, który wymaga od algorytmu odwiedzenia, sprawdzenia i / lub aktualizacji każdego nieodwiedzonego węzła w struktura drzewiasta. Algorytm BFS działa na podobnej zasadzie.
• Algorytm jest przydatny do analizy węzłów na grafie i konstruowania najkrótszej ścieżki przechodzenia przez nie.
• Algorytm przechodzi przez wykres w najmniejszej liczbie iteracji i w najkrótszym możliwym czasie.
• BFS wybiera pojedynczy węzeł (punkt początkowy lub źródłowy) na wykresie, a następnie odwiedza wszystkie węzły sąsiadujące z wybranym węzłem. BFS uzyskuje dostęp do tych węzłów jeden po drugim.
• Odwiedzone i zaznaczone dane są umieszczane w kolejce przez BFS. Kolejka działa na zasadzie pierwsze weszło pierwsze wyszło. Stąd element umieszczony na wykresie jako pierwszy jest usuwany jako pierwszy i w rezultacie drukowany.
• Algorytm BFS nigdy nie może zostać złapany w nieskończoną pętlę.
• Dzięki wysokiej precyzji i solidnej implementacji BFS jest używany w wielu rzeczywistych rozwiązaniach, takich jak sieci P2P, roboty sieciowe, i nadawanie w sieci.