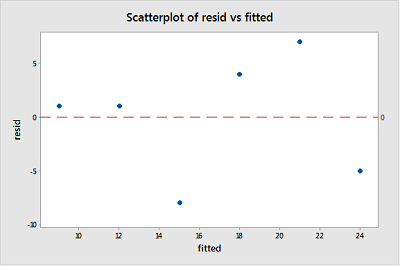
Podczas przeprowadzania analizy reszt najczęściej tworzonym wykresem jest „wykres reszty versus dopasowania”. Jest to wykres punktowy reszt na osi y i dopasowanych wartości (oszacowanych odpowiedzi) na osi x. Wykres służy do wykrywania nieliniowości, nierównych wariancji błędów i wartości odstających.
Spójrzmy na przykład, aby zobaczyć, jak wygląda „grzeczny” wykres resztkowy. Niektórzy badacze (Urbano- Marquez i in., 1989) byli zainteresowani ustaleniem, czy spożycie alkoholu jest liniowo związane z siłą mięśni. Naukowcy zmierzyli całkowite spożycie alkoholu (x) w ciągu całego życia na losowej próbie n = 50 alkoholików. siła (y) mięśnia naramiennego w niedominującym ramieniu każdej osoby. Dopasowany wykres liniowy wynikowych danych (alcoholarm.txt) wygląda następująco:
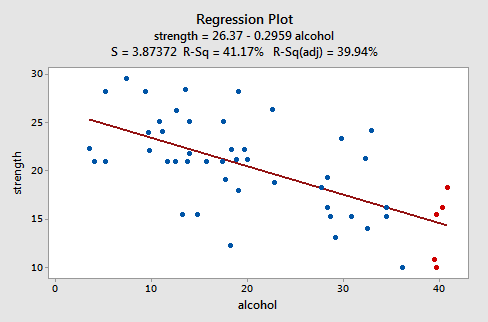
Wykres sugeruje, że istnieje malejąca liniowa zależność między alkoholem a siłą ramion. Sugeruje również, że w zbiorze danych nie ma nietypowych punktów danych. I ilustruje to, że zmienność wokół oszacowanej linii regresji jest stała, co sugeruje, że założenie równych wariancji błędu jest rozsądne.
Oto „jak wygląda odpowiedni wykres reszty w funkcji dopasowania dla zbioru danych” s prosty model regresji liniowej z siłą ramion jako odpowiedzią i wskaźnikiem spożycia alkoholu:
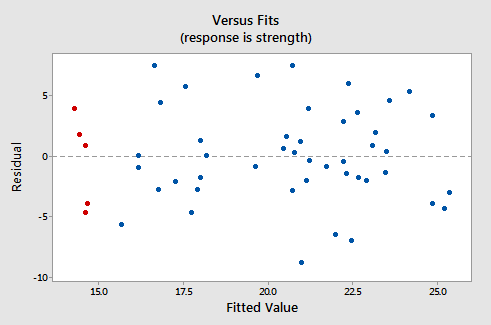
Zauważ, że zgodnie z definicją, reszty pojawiają się na osi y, a dopasowane wartości – na osi x. Powinieneś być w stanie spojrzeć wstecz na wykres punktowy danych i zobaczyć, w jaki sposób punkty danych tam odpowiadają punktom danych na wykresie reszta versus pasowania tutaj. Jeśli masz z tym problem, spójrz na pięć punktów danych na oryginalnym wykresie punktowym, które pojawiają się na czerwono. Zwróć uwagę, że przewidywana odpowiedź (dopasowana wartość) tych mężczyzn (których spożycie alkoholu wynosi około 40) wynosi około 14 . Zwróć także uwagę na wzór, w którym pięć punktów danych odchyla się od oszacowanej linii regresji.
Teraz spójrz, jak i gdzie te pięć punktów danych pojawia się na wykresie reszty w porównaniu z dopasowaniami. Ich dopasowana wartość wynosi około 14 a ich odchylenie od linii residual = 0 ma ten sam wzorzec, co ich odchylenie od oszacowanej linii regresji. Czy widzisz związek? Linia 0 odpowiada oszacowanej linii regresji.
Ten wykres jest klasycznym przykładem dobrze zachowującego się wykresu reszty vs. pasowania. Oto cechy dobrze zachowującego się wykresu reszta vs. zasugeruj stosowność prostego Model regresji liniowej:
- Reszty „odbijają się losowo” wokół linii 0. Sugeruje to, że założenie, że zależność jest liniowa, jest rozsądne.
- Reszty z grubsza tworzą „poziome pasmo” wokół linii 0. Sugeruje to, że wariancje składników błędów są równe.
- Żadna reszta „nie wyróżnia się” z podstawowego losowego wzoru reszt. Sugeruje to, że nie ma wartości odstających.
Ogólnie rzecz biorąc, chcesz, aby wykresy reszty i pasowań wyglądały podobnie do powyższego wykresu. Nie zapominaj jednak, że interpretacja tych wykresów jest subiektywna. Z mojego doświadczenia wynika, że uczniowie uczący się analizy resztkowej po raz pierwszy mają tendencję do nadinterpretowania tych wykresów, patrząc na każdy zwrot akcji jako coś potencjalnie kłopotliwego. Szczególnie będziesz chciał należy uważać, aby nie przykładać zbyt dużej wagi do wykresów resztowych i dopasowań opartych na małych zestawach danych. Czasami zbiory danych są po prostu zbyt małe, aby interpretacja wykresu reszty vs. pasowania była warta zachodu. Nie martw się! Z praktyką nauczysz się „czytać” te wykresy.