Załóżmy, że powietrze jest wpompowywane w gładką okrągłą rurkę, która ma stałą średnicę z wyjątkiem sekcji pośrodku, gdzie rura się zwęża do połowy średnicy, a następnie ponownie się rozszerza. Załóżmy, że wszystkie zmiany średnicy zachodzą płynnie, a powietrze przepływa równomiernie w dół rury, bez wirów i turbulencji.
Ćwiczenie
gdzie w rurze się spodziewasz ciśnienie, aby być największym?
Odpowiedź
Większość ludzi pytała o to po raz pierwszy, przewidując, że ciśnienie będzie największe w wąskiej części rury. Ale w rzeczywistości, jeśli faktycznie przeprowadzimy eksperyment, umieszczając manometry w różnych punktach wzdłuż rury, stwierdzimy, wbrew intuicji, że ciśnienie powietrza jest najniższe tam, gdzie powietrze porusza się najszybciej!

Aby zobaczyć, jak to może wyglądać, zastosujemy techniki, które opracowaliśmy, aby sprawdzić, jak zmieniało się ciśnienie w stacjonarnym płynie. Pamiętaj, że sposób, w jaki to zrobiliśmy, polegał na narysowaniu schematu swobodnego ciała dla małego cylindra płynu. Ponieważ ten mały cylinder był w spoczynku, całkowita siła działająca na niego wynosiła zero, więc ciśnienie netto równoważyło ciężar. Rozważ teraz płynnie poruszający się płyn. Warto zwizualizować przepływ, rysując linie opływowe, linie w taki sposób, aby ich kierunek był kierunkiem przepływu płynu w każdym punkcie.

W rzeczywistości te linie opływowe nie tylko wskazują kierunek przepływu płynu, ale także dają wyobrażenie o prędkości – gdy zbliżają się do siebie, płyn musi poruszać się szybciej, ponieważ płynie taka sama ilość płynu przez węższy region. Wyobraź sobie teraz cylinder powietrza poruszający się wzdłuż rury, którego oś jest równoległa do linii opływu. Oczywiście musi przyspieszyć, gdy wchodzi do wąskiej części rury – ponieważ ta sama ilość powietrza przepływa przez wąską część co szeroka, musi być szybsza.
Ale jeśli mała cylinder płynu przyspiesza, musi na niego działać siła popychająca go od tyłu.
Jego waga nie ma tutaj znaczenia, ponieważ porusza się poziomo. Dlatego jedyną siłą działającą na nią jest nacisk i musimy stwierdzić, że nacisk na jego plecy jest większy niż nacisk na jego przód. Dlatego ciśnienie musi spaść przy wejściu do wąskiej części. Aby wyjaśnić, co się dzieje, narysujemy raczej duży cylinder:
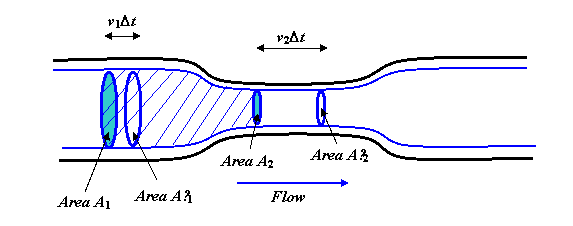
Płyn płynie równomiernie i płynnie rura. Grube niebieskie linie są liniami opływowymi, w rzeczywistości powinieneś sobie wyobrazić obracanie całego diagramu wokół centralnej osi, aby uzyskać trójwymiarowy obraz, a niebieskie linie stałyby się cylindrem z węższą sekcją „szyjki”, odzwierciedlając kształt
Rozważmy teraz masę płynu w pokazanych liniach prądu i zamkniętą na dwóch końcach okrągłymi obszarami A1 i A2. Szybkość przepływu płynu przez A1 musi być taka sama jak prędkość przepływ przez A2, ponieważ przy stałym przepływie płyn nie może gromadzić się w środku (ani stamtąd też się wyczerpywać). Objętość przepływająca przez A1 w ciągu jednej sekundy to v1A1. (Aby to zobaczyć, wyobraź sobie długą prostą rurę bez wąskiego Jeśli płyn przepływa z prędkością, powiedzmy 3 metrów na sekundę, to w ciągu jednej sekundy przepłynie cały płyn, który znajdował się w promieniu 3 metrów od obszaru A1 po stronie wlotowej.)
A więc, przepływ przez A1 równa się przepływ przez A2, \
(Przypis: Być może warto wspomnieć, że niejawnie zakładamy prędkość ty jest taka sama we wszystkich punktach obszaru A1. Każdy prawdziwy płyn ma pewną lepkość (tarcie) i będzie poruszał się wolniej w pobliżu boków rury niż w środku. Omówimy to później. Na razie rozważamy „idealny” płyn, termin używany, gdy pomija się lepkość. W rzeczywistości otrzymany wynik jest w porządku – moglibyśmy wziąć mały obszar A1 daleko od boków, tak aby prędkość była to samo dla całego obszaru, ale dałoby to znacznie mniej przejrzysty diagram.)
Jesteśmy teraz gotowi do zbadania wzrostu energii kinetycznej płynu, gdy przyspiesza on do wąskiej części, i zrozum, w jaki sposób różnica ciśnień wykonała pracę niezbędną do jej przyspieszenia.
\
Jedynym możliwym źródłem tego wzrostu energii jest praca wykonywana przez ciśnienie we wciskaniu płynu do wąska część.
\
Więc to jest praca wykonywana na naszym kawałku płynu przez płyn wypychający go od tyłu – ale to nie koniec historii, ponieważ nasza część sam płyn działa, wypychając płyn przed siebie, więc aby znaleźć całkowity wzrost energii naszego kawałka, musimy odjąć jego zewnętrzną pracę.Oznacza to, że całkowita praca wykonana przez ciśnienie na naszym płynie wynosi
\
pamiętając, że \ (A_1v_1 = A_2v_2 \).
Ta praca musi być równa zmiana energii kinetycznej, a więc
\
z czego
\
To jest równanie Bernoulliego.
\.
Współautorzy i atrybucje
- Michael Fowler (profesor belek, Wydział Fizyki, Uniwersytet Wirginii)