A som is het resultaat van een optelling. Als u bijvoorbeeld 1, 2, 3 en 4 toevoegt, krijgt u de som 10, geschreven
 |
(1)
|
De getallen die worden opgeteld, worden addends of soms summands genoemd. De sommatieoperatie kan ook worden aangegeven met behulp van een hoofdsigma met boven- en ondergrenzen geschreven boven en onder, en de index hieronder aangegeven. De bovenstaande som kan bijvoorbeeld worden geschreven
 |
(2)
|
De som van een lijst met getallen wordt geïmplementeerd als totaal.
Een som
 |
(3)
|
waarin elke term 
wordt gegeven door een vaste regel (dwz 
is een put -gedefinieerde reeks) wordt een (eindige) reeks genoemd, en als het aantal termen 
oneindig is, wordt de som een oneindige reeks genoemd (of vaak gewoon een “reeks”). Een som van de vorm
 |
(4)
|
wordt een geometrische reeks genoemd .
Voorwaarden voor convergentie van een reeks kunnen worden bepaald in de Wolfram-taal met behulp van SumConvergence.
De algemene eindige machtssom
 |
(5)
|
kan worden gegeven door de uitdrukking
 |
(6)
|
wat equivalent is aan de formule van Faulhaber, waarbij de notatie 
de hoeveelheid in vraag wordt gesteld aan de juiste macht 
en alle termen in de vorm 
worden vervangen door de overeenkomstige Bernoulli-nummers 
.
Een grappige identiteit dankzij J. Ziegenbein (pers. comm., 19 juni 2002) volgt uit de identiteit
 |
(7)
|
die kan worden geschreven
 |
(8)
|
Daarom 
kan bijvoorbeeld in de equivalente vormen worden geschreven
 |
 |
 |
(9)
|
 |
 |
 |
(10)
|
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
enzovoort.
De stelling van Nicomachus geeft als merkwaardige uitdrukking voor de machtssom 
.
Speciale sommen zijn onder andere
 |
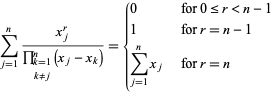(13)
|
en
 |
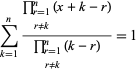(14)
|
Om de som van een reeks kwadraten te minimaliseren aantal getallen 
over een bepaald getal 
 |
 |
 |
(15 )
|
 |
 |
 |
(16)
|
neem de afgeleide.
 |
(17)
|
Oplossen voor 
geeft
 |
(18)
|
dus 
wordt geminimaliseerd wanneer 
is ingesteld op de gemeen.