Opmerking: dit artikel is oorspronkelijk gepubliceerd op 10 oktober 2014 en bijgewerkt op 27 maart 2018
Overzicht
- Begrijp k naaste buur (KNN) – een van de meest populaire algoritmen voor machine learning
- Leer de werking van kNN in python
- Kies de juiste waarde van k in eenvoudige bewoordingen
Inleiding
In de vier jaar van mijn data science-carrière heb ik meer dan 80% classificatiemodellen en slechts 15-20% regressiemodellen gebouwd. Deze verhoudingen kunnen in de hele industrie min of meer worden gegeneraliseerd. De reden achter deze voorkeur voor classificatiemodellen is dat de meeste analytische problemen het nemen van een beslissing met zich meebrengen.
Zal een klant bijvoorbeeld aantrekkelijk zijn of niet, als we klant X voor digitale campagnes, of de klant een hoog potentieel heeft of niet, enz. Deze analyses zijn inzichtelijker en direct gekoppeld aan een implementatieroadmap.
In dit artikel zullen we het hebben over een andere veelgebruikte classificatietechniek voor machine learning, genaamd K-naaste buren (KNN). Onze focus zal voornamelijk liggen op hoe het algoritme werkt en hoe de invoerparameter de uitvoer / voorspelling beïnvloedt.
Opmerking: mensen die liever via videos leren, kunnen hetzelfde leren via onze gratis cursus – K- Naaste buren (KNN) algoritme in Python en R. En als je een complete beginner bent in datawetenschap en machine learning, bekijk dan ons Certified BlackBelt-programma –
- Certified AI & ML Blackbelt + Program
Inhoudsopgave
- Wanneer gebruiken we het KNN-algoritme?
- Hoe werkt de KNN-algoritme werkt?
- Hoe kiezen we de factor K?
- Opsplitsen – Pseudo-code van KNN
- Implementatie in Python helemaal opnieuw
- Ons model vergelijken met scikit-learn
Wanneer gebruiken we het KNN-algoritme?
KNN kan voor beide worden gebruikt classificatie en regressie voorspellende problemen. Het wordt echter op grotere schaal gebruikt bij classificatieproblemen in de industrie. Om elke techniek te evalueren, kijken we in het algemeen naar 3 belangrijke aspecten:
1. Gemakkelijk te interpreteren output
2. Rekentijd
3. Voorspellende kracht
Laten we een paar voorbeelden nemen om KNN in de schaal te plaatsen:
KNN-algoritme beurzen over alle parameters van overwegingen. Het wordt vaak gebruikt vanwege de gemakkelijke interpretatie en de korte rekentijd.
Hoe werkt het KNN-algoritme?
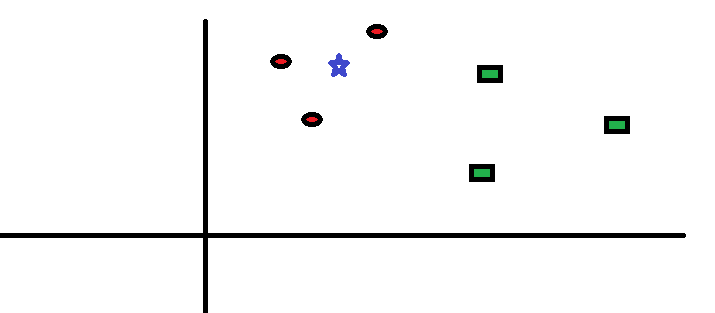
Laten we een eenvoudig voorbeeld nemen van begrijp dit algoritme. Hieronder volgt een overzicht van rode cirkels (RC) en groene vierkanten (GS):
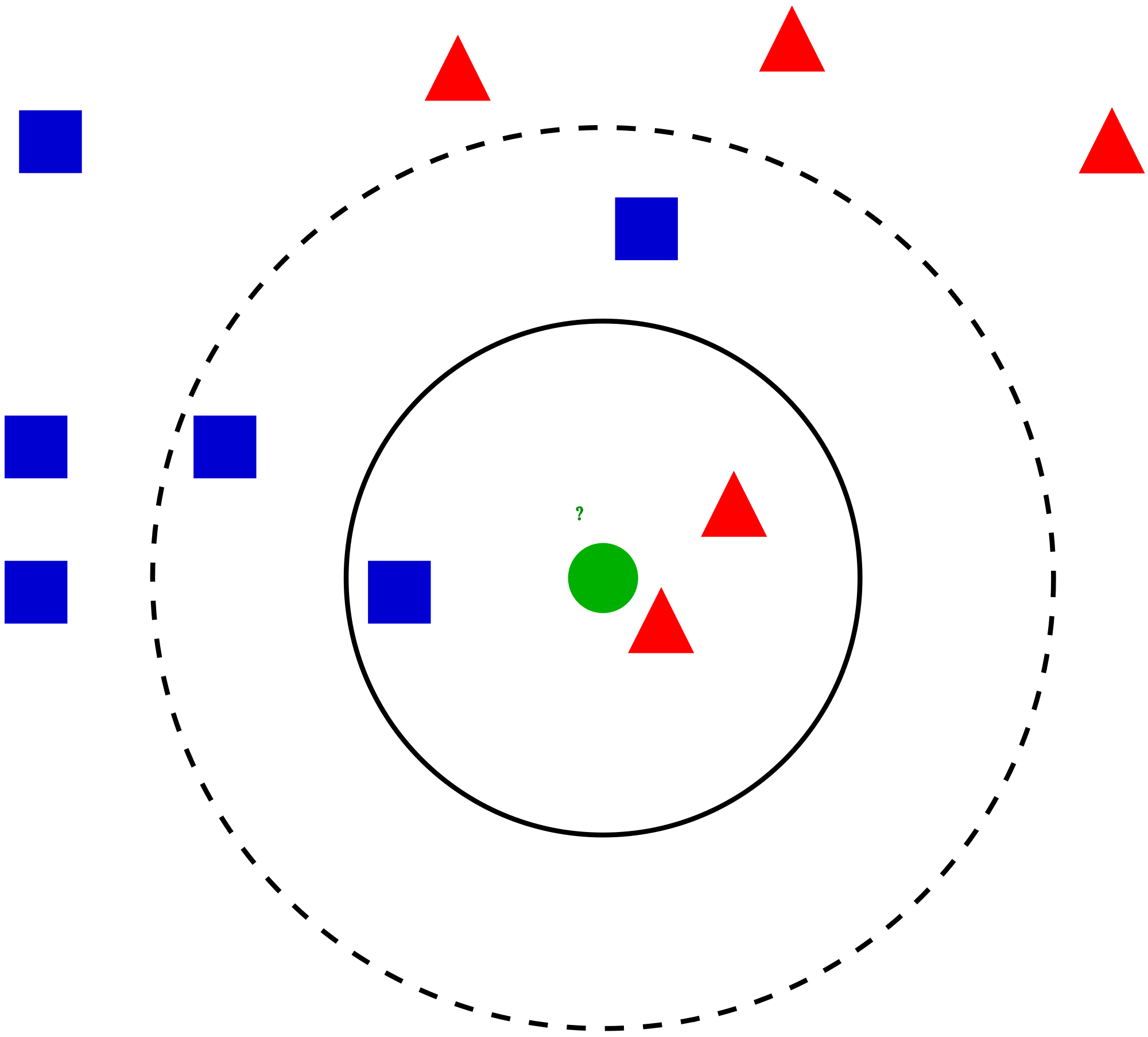
U wilt erachter komen de klasse van de blauwe ster (BS). BS kan RC of GS zijn en niets anders. De “K” is KNN-algoritme is de naaste buur waarvan we willen stemmen. Laten we zeggen K = 3. Daarom maken we nu een cirkel met BS als het middelpunt, net zo groot dat we slechts drie datapunten in het vlak omsluiten . Raadpleeg het volgende diagram voor meer details:
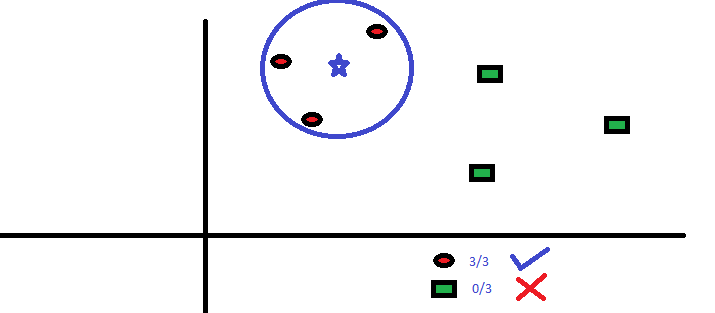De drie punten die het dichtst bij BS liggen, zijn allemaal RC. met een goed betrouwbaarheidsniveau kunnen we zeggen dat de BS tot de klasse RC zou moeten behoren. Hier werd de keuze heel duidelijk aangezien alle drie de stemmen van de naaste buur naar RC gingen. De keuze van de parameter K is erg cruciaal in dit algoritme . Vervolgens zullen we begrijpen wat de factoren zijn waarmee rekening moet worden gehouden om de beste K te concluderen.
Hoe kiezen we de factor K?
Laten we eerst proberen te begrijpen wat K precies beïnvloedt in het algoritme.Als we het laatste voorbeeld zien, gegeven het feit dat alle 6 trainingsobservaties constant blijven, kunnen we met een gegeven K-waarde grenzen stellen aan elke klasse. se grenzen zullen RC van GS scheiden. Laten we op dezelfde manier proberen het effect van waarde K op de klassengrenzen te zien. Hieronder volgen de verschillende grenzen die de twee klassen scheiden met verschillende waarden van K.
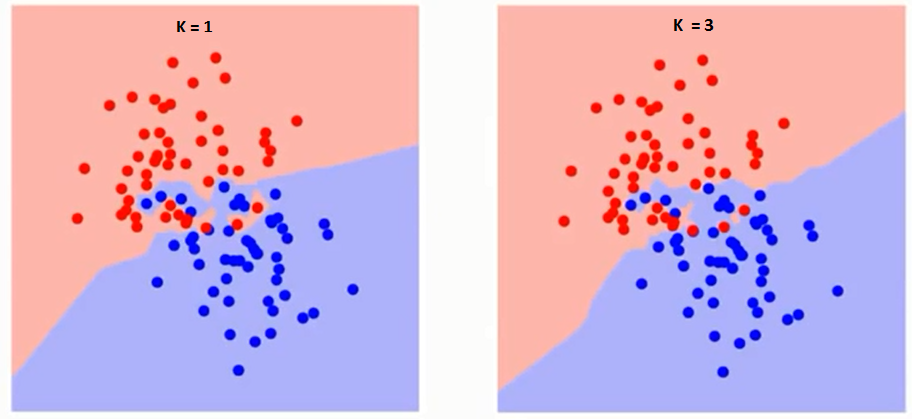
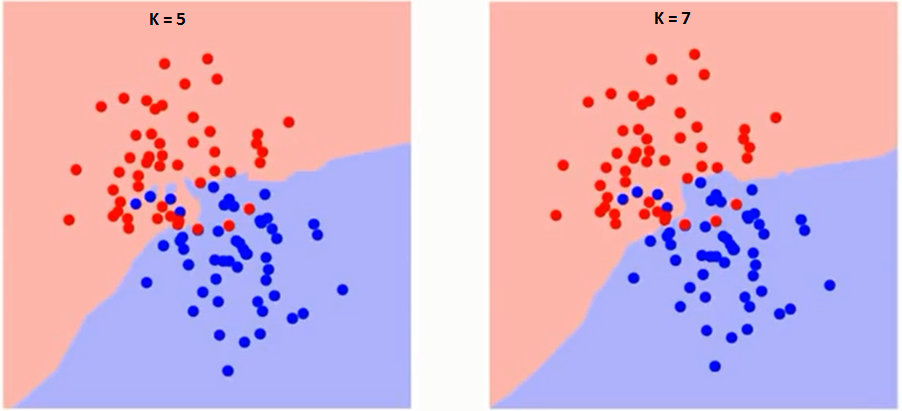
Als je goed kijkt, kun je zien dat de grens wordt vloeiender met toenemende waarde van K. Met K stijgend tot oneindig wordt het uiteindelijk helemaal blauw of helemaal rood, afhankelijk van de totale meerderheid. Het trainingsfoutpercentage en het validatiefoutpercentage zijn twee parameters die we nodig hebben om toegang te krijgen tot verschillende K-waarden. Hieronder volgt de curve voor het trainingsfoutenpercentage met een variërende waarde van K:
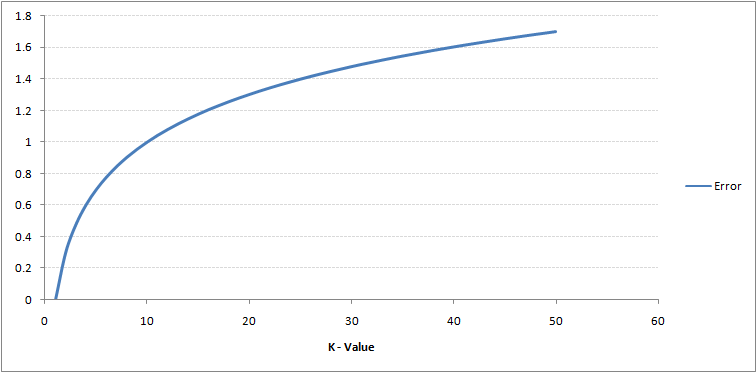Zoals u kunt zien, foutpercentage bij K = 1 is altijd nul voor het trainingsmonster.Dit komt doordat het punt dat het dichtst bij een trainingsgegevenspunt ligt, zichzelf is, waardoor de voorspelling altijd nauwkeurig is met K = 1. Als de validatiefoutcurve vergelijkbaar zou zijn geweest, zou onze keuze voor K 1 zijn geweest. Hieronder volgt de validatiefoutcurve met variërende waarde van K:
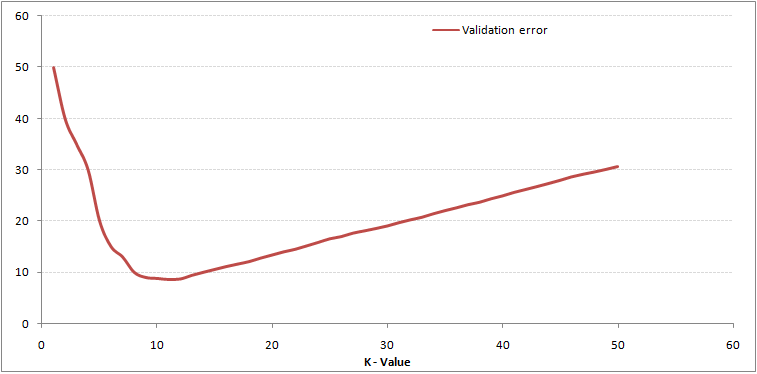Dit maakt het verhaal duidelijker. Bij K = 1 overschreden we de grenzen. Daarom neemt het foutenpercentage aanvankelijk af en bereikt het een minima. Na het minimapunt neemt het vervolgens toe met toenemende K. Om de optimale waarde van K te krijgen, kunt u de training en validatie scheiden van de initiële dataset. Zet nu de validatiefoutcurve uit om de optimale waarde van K te krijgen. Deze waarde van K moet voor alle voorspellingen worden gebruikt.
De bovenstaande inhoud kan intuïtiever worden begrepen met behulp van onze gratis cursus – K-Dichtstbijzijnde buren ( KNN) Algoritme in Python en R
Opsplitsen – Pseudo-code van KNN
We kunnen een KNN-model implementeren door de onderstaande stappen te volgen:
- Laad de gegevens
- Initialiseer de waarde van k
- Om de voorspelde klasse te krijgen, herhaal je van 1 tot het totale aantal trainingsgegevenspunten
- Bereken de afstand tussen de tests gegevens en elke rij trainingsgegevens. Hier zullen we Euclidische afstand gebruiken als onze afstandsmetriek, aangezien dit de meest populaire methode is. De andere statistieken die kunnen worden gebruikt, zijn Chebyshev, cosinus, etc.
- Sorteer de berekende afstanden in oplopende volgorde op basis van afstandswaarden
- Haal de bovenste k rijen uit de gesorteerde array
- Haal de meest voorkomende klasse van deze rijen op
- Geef de voorspelde klasse terug
Implementatie in Python helemaal opnieuw
We zullen de populaire Iris-dataset gebruiken voor het bouwen van ons KNN-model. U kunt het hier downloaden.
Ons model vergelijken met scikit-learn
We kunnen zien dat beide modellen dezelfde klasse voorspelden (Iris- virginica ) en dezelfde naaste buren (). Daarom kunnen we concluderen dat ons model werkt zoals verwacht.
Implementatie van kNN in R
Stap 1: Importeren van de data
Stap 2: Controle van de data en het gegevensoverzicht berekenen
Uitvoer
Stap 3: de gegevens splitsen
Stap 4: berekenen de Euclidische afstand
Stap 5: De functie schrijven om kNN te voorspellen
Stap 6: Het label (naam) berekenen voor K = 1
Uitvoer
For K=1 "Iris-virginica"
Op dezelfde manier kunt u andere waarden van K berekenen.
Onze kNN-voorspellende functie vergelijken met de “Class” -bibliotheek
Output
For K=1 "Iris-virginica"
We kunnen zien dat beide modellen voorspelden dezelfde klasse (Iris-virginica).
Eindnoten
Het KNN-algoritme is een van de eenvoudigste classificatie-algoritmen. Zelfs met Door deze eenvoud kan het zeer competitieve resultaten opleveren. Het KNN-algoritme kan ook worden gebruikt voor regressieproblemen. Het enige verschil van de besproken methodologie zullen gemiddelden van naaste buren gebruiken in plaats van stemmen van naaste buren. KNN kan worden gecodeerd in een enkele regel op R. Ik moet nog onderzoeken hoe we het KNN-algoritme op SAS kunnen gebruiken.
Vond u het artikel nuttig? Heeft u onlangs een andere machine learning-tool gebruikt? Bent u van plan KNN te gebruiken bij een van uw zakelijke problemen? Zo ja, vertel ons hoe u van plan bent dit aan te pakken.