Breadth First Search-algoritme (BFS) met VOORBEELD

Wat is het BFS-algoritme (breedte-eerste zoekopdracht)?

Breedte-eerste zoekopdracht (BFS) is een algoritme dat wordt gebruikt om grafieken van gegevens te maken of om boom- of traversestructuren te doorzoeken. De volledige vorm van BFS is de breedte-eerste zoekopdracht.

Het algoritme bezoekt en markeert efficiënt alle belangrijke knooppunten in een grafiek op een nauwkeurige wijze in de breedte. Dit algoritme selecteert een enkel knooppunt (beginpunt of bronpunt) in een grafiek en bezoekt vervolgens alle knooppunten grenzend aan het geselecteerde knooppunt. Onthoud dat BFS deze knooppunten een voor een benadert.

Zodra het algoritme het startknooppunt bezoekt en markeert, beweegt het naar de dichtstbijzijnde onbezochte knooppunten en analyseert deze. Eenmaal bezocht, zijn alle knooppunten gemarkeerd. Deze iteraties gaan door totdat alle knooppunten van de grafiek met succes zijn bezocht en gemarkeerd.

In deze Algorithm-zelfstudie leert u:

• Wat is BFS-algoritme (Breadth-First Search)?
• Wat zijn Graph-traversals?
• De architectuur van het BFS-algoritme
• Waarom hebben we BFS-algoritme nodig?
• Hoe werkt het BFS-algoritme?
• Voorbeeld van BFS-algoritme
• Regels van BFS-algoritme
• Toepassingen van BFS-algoritme

Wat zijn Graph-traversals?

Een grafiekdoorgang is een veelgebruikte methode om de hoekpuntpositie in de grafiek te lokaliseren. Het is een geavanceerd zoekalgoritme dat de grafiek met snelheid en precisie kan analyseren en de volgorde van de bezochte hoekpunten kan markeren. Dit proces stelt u in staat om snel elk knooppunt in een grafiek te bezoeken zonder vast te zitten in een oneindige lus.

De architectuur van het BFS-algoritme

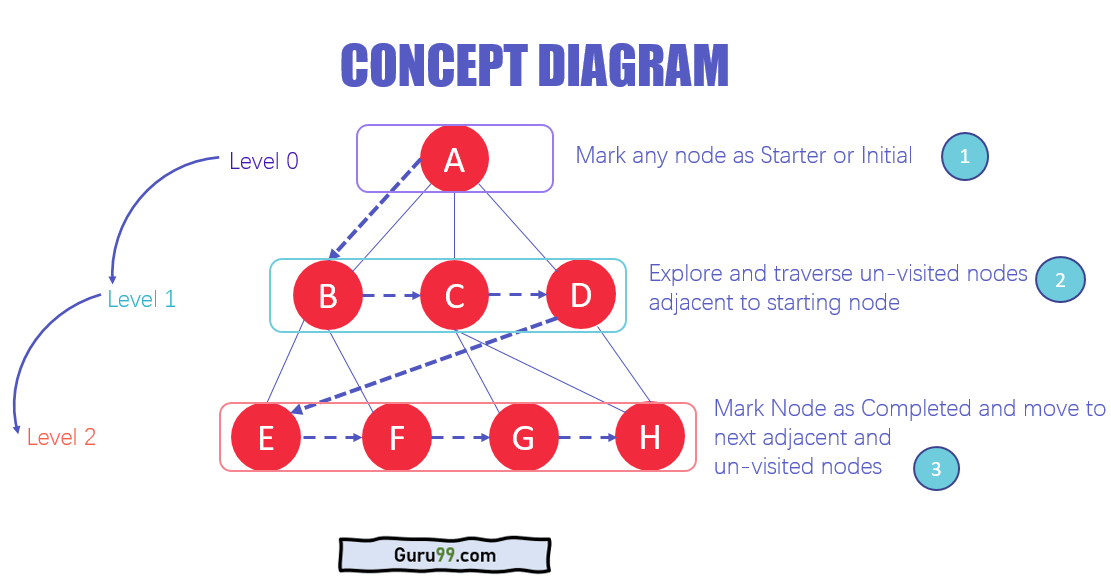
1. In de verschillende niveaus van de gegevens kunt u elk knooppunt markeren als het beginpunt of eerste knooppunt om te beginnen met doorlopen. De BFS zal het knooppunt bezoeken en het markeren als bezocht en het in de wachtrij plaatsen.
2. Nu zal het BFS de dichtstbijzijnde en niet-bezochte knooppunten bezoeken en deze markeren. Deze waarden worden ook aan de wachtrij toegevoegd. De wachtrij werkt volgens het FIFO-model.
3. Op een vergelijkbare manier worden de resterende dichtstbijzijnde en niet-bezochte knooppunten in de grafiek geanalyseerd, gemarkeerd en aan de wachtrij toegevoegd. Deze items worden bij ontvangst uit de wachtrij verwijderd en als resultaat afgedrukt.

Waarom hebben we BFS-algoritme nodig?

Er zijn talloze redenen om het BFS-algoritme te gebruiken bij het zoeken naar uw dataset. Enkele van de meest vitale aspecten die van dit algoritme uw eerste keuze maken, zijn:

• BFS is handig voor het analyseren van de knooppunten in een grafiek en het construeren van het kortste pad om deze te doorlopen.
• BFS kan door een grafiek bladeren in het kleinste aantal iteraties.
• De architectuur van het BFS-algoritme is eenvoudig en robuust.
• Het resultaat van het BFS-algoritme is zeer nauwkeurig in vergelijking met andere algoritmen.
• BFS-iteraties zijn naadloos en er is geen mogelijkheid dat dit algoritme verstrikt raakt in een oneindig lusprobleem.

Hoe werkt het BFS-algoritme?

Het doorlopen van grafieken vereist dat het algoritme elk niet-bezocht knooppunt in een boomachtige structuur bezoekt, controleert en / of actualiseert. Grafiekverplaatsingen worden gecategoriseerd op basis van de volgorde waarin ze de knooppunten in de grafiek bezoeken.

BFS-algoritme start de bewerking vanaf het eerste of startknooppunt in een grafiek en doorloopt het grondig. Zodra het met succes het eerste knooppunt doorkruist, wordt het volgende niet-doorlopen hoekpunt in de grafiek bezocht en gemarkeerd.

Daarom kun je zeggen dat alle knooppunten grenzend aan het huidige hoekpunt worden bezocht en doorlopen in de eerste iteratie. Er wordt een eenvoudige wachtrij-methodologie gebruikt om de werking van een BFS-algoritme te implementeren, en deze bestaat uit de volgende stappen:

Stap 1)

Elk hoekpunt of knooppunt in de grafiek is bekend. U kunt het knooppunt bijvoorbeeld markeren als V.

Stap 2)

In het geval dat hoekpunt V niet wordt benaderd, voeg dan hoekpunt V toe aan de BFS-wachtrij

Stap 3)

Start de BFS-zoekopdracht en markeer na voltooiing hoekpunt V als bezocht.

Stap 4)

De BFS-wachtrij is nog steeds niet leeg, verwijder daarom het hoekpunt V van de grafiek uit de wachtrij.

Stap 5)

Haal alle resterende hoekpunten op op de grafiek die grenst aan het hoekpunt V

Stap 6)

Laten we voor elk aangrenzend hoekpunt zeggen V1, voor het geval het nog niet bezocht is, voeg dan V1 toe aan de BFS-wachtrij

Stap 7)

BFS zal V1 bezoeken en markeren als bezocht en verwijderen uit de wachtrij.

Voorbeeld BFS-algoritme

Stap 1)

Je hebt een grafiek van zeven cijfers van 0 – 6.

Stap 2)

0 of nul is gemarkeerd als een hoofdknooppunt.

Stap 3)

0 wordt bezocht, gemarkeerd en ingevoegd in de datastructuur van de wachtrij.

Stap 4)

De resterende 0 aangrenzende en niet-bezochte knooppunten worden bezocht, gemarkeerd en in de wachtrij ingevoegd.

Stap 5)

Doorlopende iteraties worden herhaald totdat alle knooppunten zijn bezocht.

Regels van BFS-algoritme

Hier zijn belangrijke regels voor het gebruik van BFS-algoritme:

• Een wachtrij (FIFO-First in First Out) datastructuur wordt gebruikt door BFS.
• U markeert elk knooppunt in de grafiek als root en begint de gegevens ervan te doorlopen.
• BFS doorloopt alle knooppunten in de grafiek en blijft ze neerzetten als voltooid.
• BFS bezoekt een aangrenzende niet-bezochte knoop, markeert deze als voltooid en voegt deze in een wachtrij in.
• Verwijdert het vorige hoekpunt uit de wachtrij voor het geval er geen aangrenzende hoek wordt gevonden.
• Het BFS-algoritme wordt herhaald totdat alle hoekpunten in de grafiek met succes zijn doorlopen en gemarkeerd als voltooid.
• Er zijn geen lussen veroorzaakt door BFS tijdens het doorlopen van gegevens vanaf een knooppunt.

Toepassingen van BFS-algoritme

Laten we eens kijken bekijk enkele van de real-life applicaties waar een implementatie van een BFS-algoritme zeer effectief kan zijn.

• Ongewogen grafieken: BFS-algoritme kan eenvoudig het kortste pad en een minimale spanning tree creëren om alle de hoekpunten van de grafiek in de kortst mogelijke tijd met hoge nauwkeurigheid.
• P2P-netwerken: BFS kan worden geïmplementeerd om alle dichtstbijzijnde of naburige knooppunten in een peer-to-peer-netwerk te lokaliseren. Hierdoor worden de vereiste gegevens sneller gevonden .
• Webcrawlers: zoekmachines of webcrawlers kunnen gemakkelijk meerdere niveaus van indexen bouwen door BFS te gebruiken. BFS-implementatie begint bij de bron, de webpagina, en bezoekt vervolgens alle links van die bron .
• Navigatiesystemen: BFS kan helpen bij het vinden van alle aangrenzende locaties vanaf de hoofd- of bronlocatie.
• Netwerkuitzending ing: Een uitgezonden pakket wordt geleid door het BFS-algoritme om alle knooppunten te vinden en te bereiken waarvoor het het adres heeft.

Samenvatting

• Het doorlopen van een grafiek is een uniek proces waarbij het algoritme elk niet-bezocht knooppunt in een website moet bezoeken, controleren en / of bijwerken. boomachtige structuur. Het BFS-algoritme werkt volgens een soortgelijk principe.
• Het algoritme is handig voor het analyseren van de knooppunten in een grafiek en het construeren van het kortste pad om deze te doorlopen.
• Het algoritme doorloopt de grafiek in zo min mogelijk iteraties en in zo kort mogelijke tijd.
• BFS selecteert een enkel knooppunt (beginpunt of bronpunt) in een grafiek en bezoekt vervolgens alle knooppunten grenzend aan het geselecteerde knooppunt. BFS benadert deze knooppunten één voor één.
• De bezochte en gemarkeerde gegevens worden door BFS in een wachtrij geplaatst. Een wachtrij werkt op basis van first in first out. Daarom wordt het element dat als eerste in de grafiek is geplaatst, eerst verwijderd en als resultaat afgedrukt.
• Het BFS-algoritme kan nooit in een oneindige lus terechtkomen.
• Vanwege de hoge precisie en robuuste implementatie wordt BFS gebruikt in meerdere real-life oplossingen zoals P2P-netwerken, webcrawlers, en netwerkuitzending.