Hoe varieert de druk met volumeverandering tijdens adiabatische uitzetting en compressie in een ideaal gas? Deze pagina is een bijlage bij onze bespreking van geluid. Lucht onder atmosferische druk is een bijna ideaal gas en geluidsoverdracht in lucht is bijna adiabatisch voor normale frequenties en transmissieafstanden. (We komen hieronder terug op deze aanname.)
De eerste wet van de thermodynamica relateert de verandering in interne energie dU aan het werk dW gedaan door een systeem en de warmte dQ die eraan wordt toegevoegd.
dU = dQ – dW
Per definitie, in een adiabatisch proces, wordt de warmte-uitwisseling dQ = 0. Dit in de eerste wet vervangen en opnieuw rangschikken geeft
0 = dQ = dU + dW
De tweede term is eenvoudig: het werk dat gedaan wordt dW wanneer een systeem zijn volume V met dV verandert, is PdV.
De eerste term kan verband houden met de soortelijke warmte, die wordt gedefinieerd als de warmte die wordt toegevoegd per eenheid van temperatuurverandering per mol stof. Als we warmte bij constant volume toevoegen, dan zet het gas niet uit en dus “werkt het niet. Dus de toegevoegde warmte verhoogt de interne energie U. Dus volgt die definitie dat de soortelijke warmte bij constant volume , waarbij n het aantal mol is. Daarom
Nu is de toestandsvergelijking van een ideaal gas
nRT = PV ( ii)
waarbij R de gasconstante is. Afgeleiden nemen geeft
We kunnen nu vergelijkingen (i) en (iii) combineren om T. (i) en (ii) geef respectievelijk deze uitdrukkingen voor ncv dT:
Het verzamelen van de PdV- en VdP-termen geeft
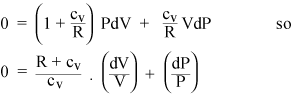
Als het gas nu ideaal is, is zijn interne energie helemaal kinetisch, dus de interne energie U hangt alleen af van T. Uit de toestandsvergelijking van een ideaal gas (ii) kunnen we berekenen het werk dW gedaan onder constante druk: het is gewoon PdV = nRdT. Dus als we warmte toevoegen aan een gas met constante druk, moeten we RdT extra verwarmen voor elke mol gas, naast de warmte die we bij constant volume zouden moeten toevoegen. De soortelijke warmte van een ideaal gas bij constante druk is dus gewoon cP = cv + R. De verhouding van de specifieke warmte krijgt een standaardsymbool:
. Dus we hebben
(iv)
Dit is het belangrijkste resultaat dat we nodig hebben om geluidsgolven te bespreken: we hebben zojuist aangetoond dat de proportionele verandering in druk – γ maal de proportionele verandering in volume of γ maal de proportionele verandering in dichtheid is.
Laten we hier echter niet stoppen, want we zijn slechts een paar regels verwijderd van een belangrijk resultaat. We weten dat d (ln x) = dx / x (zie calculus voor een bewijs). Dus we kunnen schrijven de voorgaande vergelijking als
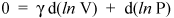
en herschik het om
(v)
Voor een adiabatisch proces in een ideaal gas,
. (vi)
Bij nader inzien gaat u ermee akkoord dat cP > cV: At constant volume, alle th De warmte die je erin stopt, gaat naar het verhogen van de interne energie en dus naar de temperatuur. Bij constante druk moet u niet alleen de warmte inbrengen die de interne energie verhoogt, maar ook een hoeveelheid warmte die gelijk is aan het werk dat wordt gedaan wanneer het systeem thermische uitzetting ondergaat. Voor lucht is γ ongeveer 1,4.
Natuurlijk kunnen we nu substitueren in (vi) van de toestandsvergelijking (ii) om te zien hoe P en T of T en V gerelateerd zijn voor een adiabatisch proces.
Wanneer is geluid adiabatisch?
We hebben hierboven vermeld dat “geluidsoverdracht in lucht bijna adiabatisch is voor normale frequenties en transmissieafstanden”. Wanneer mislukt dit? Bij de drukmaxima in een geluidsgolf is de temperatuur hoog. We verwachten dus dat er wat warmte zal diffunderen naar de aangrenzende drukminima. Natuurlijk is er in een halve periode van een geluidsgolf niet veel tijd voor warmte om een halve golflengte te verspreiden. De tijd die de warmte nodig heeft om te diffunderen, is echter het kwadraat van de afstand. Dit proces is dus minder verwaarloosbaar voor hoge frequenties, omdat de kortere halve golflengte de kortere halve periode ruimschoots compenseert. Deze diffusie haalt mechanische energie uit de golf, vooral bij hoge frequenties, en het effect neemt toe met de transmissieafstand.Om deze reden (en soms andere) zijn verre geluiden niet alleen minder luid, maar ook minder helder dan dichtbij.