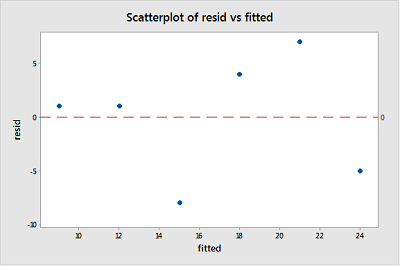
Bij het uitvoeren van een residu-analyse is een “residuals versus fits-plot” de meest gemaakte plot. Het is een spreidingsdiagram van residuen op de y-as en aangepaste waarden (geschatte responsen) op de x-as. De plot wordt gebruikt om niet-lineariteit, ongelijke foutvarianties en uitschieters te detecteren.
Laten we een voorbeeld bekijken om te zien hoe een “braaf” restdiagram eruitziet. Sommige onderzoekers (Urbano- Marquez, et al., 1989) waren geïnteresseerd in het bepalen of alcoholgebruik lineair gerelateerd was aan spierkracht. De onderzoekers maten de totale consumptie van alcohol gedurende de hele levensduur (x) op een willekeurige steekproef van n = 50 alcoholische mannen. Ze maten ook de kracht (y) van de deltaspier in de niet-dominante arm van elke persoon. Een passende lijnplot van de resulterende gegevens, (alcoholarm.txt), ziet er als volgt uit:
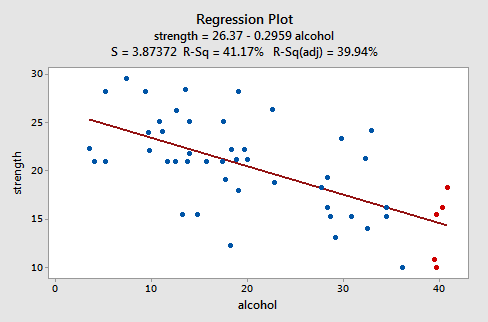
De plot suggereert dat er een afnemende lineaire relatie is tussen alcohol en armkracht. Het suggereert ook dat er geen ongebruikelijke datapunten in de dataset zijn. En het illustreert dat de variatie rond de geschatte regressielijn constant is, wat suggereert dat de aanname van gelijke foutvarianties redelijk is.
Hier is hoe de corresponderende residuen versus passingen plot eruit ziet voor de dataset s eenvoudig lineair regressiemodel met armkracht als respons en niveau van alcoholgebruik als voorspeller:
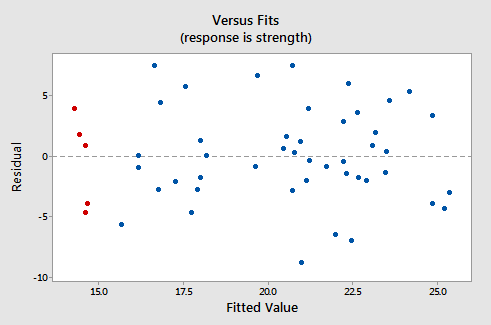
Merk op dat, zoals gedefinieerd, de residuen op de y-as verschijnen en de aangepaste waarden op de x-as. U zou in staat moeten zijn om terug te kijken naar het spreidingsdiagram van de gegevens en te zien hoe de datapunten daar overeenkomen met de datapunten in het residu versus fit-diagram hier. Als u daar problemen mee heeft, kijk dan naar de vijf gegevenspunten in het oorspronkelijke spreidingsdiagram die in rood worden weergegeven. Merk op dat de voorspelde respons (gepaste waarde) van deze mannen (met een alcoholconsumptie van rond de 40) ongeveer 14 is. Let ook op het patroon waarin de vijf datapunten afwijken van de geschatte regressielijn.
Kijk nu hoe en waar deze vijf datapunten verschijnen in de residuals versus fits-plot. Hun aangepaste waarde is ongeveer 14 en hun afwijking van de lijn residual = 0 deelt hetzelfde patroon als hun afwijking van de geschatte regressielijn. Zie je het verband? Elk gegevenspunt dat direct op de geschatte regressielijn valt, heeft een residu van 0. Daarom heeft het residu = 0-lijn komt overeen met de geschatte regressielijn.
Deze plot is een klassiek voorbeeld van een braaf residu-vs.-fit-plot. Hier zijn de kenmerken van een goed-gedragen residu-vs.-fit-plot en wat deze suggereren over de geschiktheid van de simpl Het lineaire regressiemodel:
- De residuen “stuiteren willekeurig” rond de 0-lijn. Dit suggereert dat de aanname dat het verband lineair is redelijk is.
- De residuen vormen ruwweg een “horizontale band” rond de 0-lijn. Dit suggereert dat de varianties van de fouttermen gelijk zijn.
- Geen enkel residu “onderscheidt” zich van het willekeurige basispatroon van residuen. Dit suggereert dat er geen uitschieters zijn.
Over het algemeen wilt u dat uw residuele vs. passende plots er ongeveer zo uitzien als de bovenstaande plot. Vergeet echter niet dat het interpreteren van deze plots subjectief is. Mijn ervaring is dat studenten die voor het eerst residuale analyse leren, de neiging hebben om deze plots te veel te interpreteren en elke draai en draai te beschouwen als iets dat potentieel vervelend is. Je zult vooral willen dat wees voorzichtig dat u niet te veel gewicht hecht aan residuale vs. passende plots op basis van kleine gegevenssets. Soms zijn de datasets gewoon te klein om interpretatie van een residuals vs. fits-plot de moeite waard te maken. Maak u geen zorgen! U zult – met oefening – leren hoe u deze plots moet “lezen”.