Stel dat lucht door een gladde ronde buis wordt gepompt, die een constante diameter heeft, behalve een gedeelte in het midden waar de buis smaller wordt tot de helft van de diameter en wordt dan weer breder. Veronderstel dat alle veranderingen in diameter soepel verlopen en dat de lucht gestaag door de buis stroomt, zonder wervelingen of turbulentie.
Oefening
waar in de buis verwacht u de druk om het grootst te zijn?
Antwoord
De meeste mensen die dit voor het eerst vroegen, voorspellen dat de druk het grootst zal zijn in het smalle gedeelte van de buis. Maar in feite, als we het experiment echt doen, door manometers op verschillende punten langs de buis te plaatsen, ontdekken we, tegen intuïtief in, dat de luchtdruk het laagst is waar de lucht het snelst beweegt!

Om te zien hoe dit zou kunnen zijn, zullen we toepassen de technieken die we hebben ontwikkeld om te ontdekken hoe de druk varieert in een stilstaande vloeistof. Onthoud de manier waarop we dat deden door een vrij lichaamsdiagram te tekenen voor een kleine cilinder met vloeistof. Omdat deze kleine cilinder in rust was, was de totale kracht erop nul, dus de netto druk balanceerde het gewicht. Overweeg nu een gestaag bewegende vloeistof. Het is handig om de stroom te visualiseren door in stroomlijnen te tekenen, lijnen zodanig dat hun richting de richting is waarin de vloeistof op elk punt beweegt.

Deze stroomlijnen vertellen je niet alleen in welke richting de vloeistof beweegt, maar geven ook een idee van de snelheid: waar ze dichter bij elkaar komen, moet de vloeistof sneller bewegen, omdat dezelfde hoeveelheid vloeistof stroomt door een smallere regio. Stel je nu een cilinder van lucht voor die langs de buis beweegt, met zijn as evenwijdig aan de stroomlijn. Het is duidelijk dat het sneller moet gaan als het het smalle deel van de buis binnengaat – aangezien dezelfde hoeveelheid lucht door het smalle deel stroomt als het brede deel, moet het sneller gaan.
Maar als het kleine deel vloeistofcilinder versnelt, er moet op worden ingewerkt door een kracht die het van achteren duwt.
Het gewicht is hier niet relevant, aangezien het horizontaal beweegt. Daarom is de enige kracht die erop inwerkt de druk, en we moeten concluderen dat de druk op zijn rug groter is dan de druk op zijn voorkant. Daarom moet de druk dalen bij het betreden van het smalle gedeelte. Om duidelijker te maken wat er aan de hand is, zullen we een vrij grote cilinder tekenen:
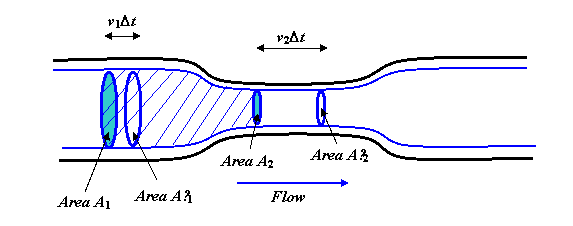
De vloeistof stroomt gestaag en soepel langs de pijp. De dikke blauwe lijnen zijn stroomlijnen, in feite zou je je moeten voorstellen dat je het hele diagram rond de centrale as draait om een driedimensionaal beeld te krijgen, en de blauwe lijnen zouden een cilinder worden, met een smaller hals-gedeelte, in navolging van de vorm van de Beschouw nu de vloeistofmassa binnen de getoonde stroomlijnen en aan de twee uiteinden afgedekt door de cirkelvormige gebieden A1 en A2. De stroomsnelheid van vloeistof over A1 moet hetzelfde zijn als de snelheid van stroom over A2, omdat bij een gestage stroom vloeistof zich niet in het midden kan opstapelen (of vanaf daar ook leeg kan raken). Het volume dat in één seconde over A1 stroomt, is v1A1. (Om dit te zien, stel je een lange rechte buis voor zonder een smalle Als de vloeistof met een snelheid van bijvoorbeeld 3 meter per seconde stroomt, dan zal in één seconde alle vloeistof die zich binnen 3 meter van gebied A1 aan de bovenstroomse zijde bevond, er doorheen zijn gestroomd.)
Dus, stroom over A1 is gelijk aan stroom over A2, \
(Voetnoot: het is misschien de moeite waard te vermelden dat we impliciet aannemen dat de veloci ty is op alle punten op gebied A1 hetzelfde. Elke echte vloeistof heeft enige viscositeit (wrijving) en zal bij de zijkanten van de buis langzamer bewegen dan in het midden. We zullen dit later bespreken. Voorlopig beschouwen we een “ideale” vloeistof, de term die wordt gebruikt wanneer men viscositeit negeert. Het resultaat dat we afleiden is in feite ok – we hadden een klein gebied A1 ver weg van de zijkanten kunnen nemen, zodat de snelheid hetzelfde voor het hele gebied, maar dat zou een veel minder duidelijk diagram hebben opgeleverd.)
We zijn nu klaar om de toename in kinetische energie van de vloeistof te onderzoeken terwijl deze versnelt tot in het smalle deel, en begrijp hoe het drukverschil het werk deed dat nodig was om het te versnellen.
\
De enige mogelijke bron voor deze toename van energie is het werk dat wordt gedaan door druk om de vloeistof in het smalle gedeelte.
\
Dit is dus werk dat wordt gedaan aan ons brok vloeistof door de vloeistof die het van achteren duwt – maar dat is niet het einde van het verhaal, want ons brok van vloeistof zelf werkt door de vloeistof ervoor te duwen, dus om de totale toename van de energie van onze brok te vinden, moeten we het externe werk dat het doet aftrekken.Dat wil zeggen, het totale werk dat wordt gedaan door druk op onze vloeistof is
\
denk eraan dat \ (A_1v_1 = A_2v_2 \).
Dit uitgevoerde werk moet gelijk zijn aan de verandering in kinetische energie, dus
\
waaruit
\
Dit is de vergelijking van Bernoulli.
\.
Bijdragers en attributen
- Michael Fowler (Beams Professor, Department of Physics, University of Virginia)