La oss analysere en enkel seriekrets og bestemme spenningsfallet over individuelle motstander:
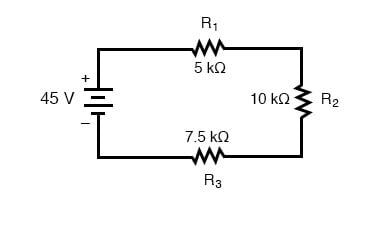

Fra de gitte verdiene for individuelle motstander kan vi bestemme en total kretsmotstand, vel vitende at motstander legger til i serie:
Bestem total kretsmotstand

Herfra kan vi bruke Ohms lov (I = E / R) for å bestemme totalstrømmen, som vi vet vil være den samme som hver motstandsstrøm, strømmen er lik i alle deler av en seriekrets:

Bruk Ohms lov for å beregne strøm
Nå som vi vet at kretsstrømmen er 2 mA, kan vi bruke Ohms lov (E = IR) for å beregne spenningen over hver motstand:

Det bør være tydelig at spenningsfallet over hver motstand er proporsjonal med motstanden, gitt at strømmen er den samme gjennom alle motstandene. Legg merke til hvordan spenningen over R2 er dobbelt så stor som spenningen over R1, akkurat som motstanden til R2 er dobbelt så stor som R1.
Hvis vi skulle endre den totale spenningen, ville vi finne denne proporsjonaliteten av spenningen dråper forblir konstant:

Løsning av spenningsfallforhold
Spenningen over R2 er fortsatt nøyaktig to ganger det til R1s fall, til tross for at kildespenningen har endret seg. Proporsjonaliteten til spenningsfall (forholdet mellom hverandre) er strengt tatt en funksjon av motstandsverdier.
Med litt mer observasjon blir det tydelig at spenningsfallet over hver motstand også er en fast andel av forsyningsspenningen. Spenningen over R1 var for eksempel 10 volt når batteriet var 45 volt. Når batterispenningen ble økt til 180 volt (4 ganger så mye), økte også spenningsfallet over R1 med en faktor på 4 (fra 10 til 40 volt). Forholdet mellom R1s spenningsfall og total spenning endret seg imidlertid ikke:

Likeledes ingen av de andre spenningsfallforhold endret med økt forsyningsspenning enten:

Spenningsdelerformel
Av denne grunn , kalles en seriekrets ofte en spenningsdeler for sin evne til å proporsjonere – eller dele – den totale spenningen i brøkdeler med konstant forhold. Med litt algebra kan vi utlede en formel for å bestemme seriemotstandsspenningsfall gitt ingenting mer enn total spenning, individuell motstand og total motstand:

Forholdet mellom individuell motstand og total motstand er det samme som forholdet mellom individuelt spenningsfall og total forsyningsspenning i en spenningsdelerkrets. Dette er kjent som formelen for spenningsdeler, og det er en snarvei for å bestemme spenningsfall i en seriekrets uten å gå gjennom gjeldende beregninger av Ohms lov.
Eksempel på bruk av spenningsdelerformel
Ved å bruke denne formelen kan vi analysere eksemplet på kretsens spenningsfall i færre trinn:


Spenning – delende komponenter
Spenningsdelere finner bred anvendelse i elektriske målerkretser, der spesifikke kombinasjoner av seriemotstander brukes til å «dele ”En spenning i nøyaktige proporsjoner som en del av en spenningsmåleenhet.

Potensiometre som spenningsdelende komponenter
En enhet som ofte brukes som en spenningsdelende komponent er potensiometeret, som er en motstand med et bevegelig element plassert av en manuell knott eller spak. Det bevegelige elementet, vanligvis kalt en visker, kommer i kontakt med en motstandsstr ip av materiale (ofte kalt lysbildetråden hvis den er laget av resistiv metalltråd) når som helst valgt av den manuelle kontrollen:

Vindusviskerkontakten er det pilen som vender mot venstre, tegnet i midten av det vertikale motstandselementet. Når den flyttes opp, kommer den i kontakt med den resistive stripen nærmere terminal 1 og lenger bort fra terminal 2, senker motstanden til terminal 1 og øker motstanden til terminal 2. Når den flyttes ned, oppnås den motsatte effekten. Motstanden målt mellom klemmene 1 og 2 er konstant for hvilken som helst viskerposisjon.
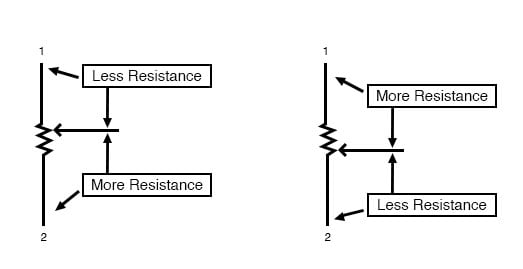
Roterende vs. lineære potensiometre
Her vises interne illustrasjoner av to potensiometertyper, roterende og lineære.
Lineære potensiometre

Noen lineære potensiometre aktiveres med rett bevegelse av en spak eller skyveknapp. Andre, som den som er avbildet i forrige illustrasjon, aktiveres av en skrue for finjusteringsevne.De sistnevnte enhetene blir noen ganger referert til som trimpots fordi de fungerer bra for applikasjoner som krever at en variabel motstand skal «trimmes» til en viss presis verdi.
Det bør bemerkes at ikke alle lineære potensiometre har de samme terminaloppdragene. som vist i denne illustrasjonen. Med noen er viskerterminalen i midten, mellom de to endeterminalene.
Roterende potensiometer
Bildet nedenfor viser kroppskonstruksjonen til et roterende potensiometer .

Følgende fotografi viser et ekte, roterende potensiometer med eksponert visker og glidetråd for enkel visning. Akselen som beveger vindusviskeren har blitt vridd nesten helt med klokken, slik at viskeren nesten berører den venstre terminalenden av lysbildetråden:

Her er det samme potensiometeret med viskerakslen beveget seg nesten helt mot klokken slik at viskeren er nær den andre ekstreme enden av kjøringen:

Effekter av justeringer i et potensiometer i en krets
Hvis en konstant spenning påføres mellom de ytre terminalene (over lengden på glidetråden) vil viskerposisjonen tappe av en brøkdel av den påførte spenningen, som kan måles mellom viskerkontakten og en av de to andre terminalene. Brøkverdien avhenger helt av viskerens fysiske posisjon:
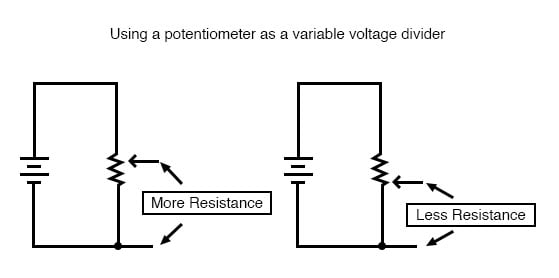
Betydningen av potensiometerapplikasjon
Akkurat som den faste spenningsdeleren, er potensiometerets spenningsdelingsforhold strengt tatt en funksjon av motstand og ikke av størrelsen på den påførte spenningen. Med andre ord, hvis potensiometerknappen eller spaken flyttes til 50 prosent (nøyaktig senter) -posisjon, vil spenningen som faller mellom viskeren og den eksterne terminalen være nøyaktig 1/2 av den påførte spenningen, uansett hvilken spenning som skjer være, eller hva potensiometerets motstand mot ende er. Med andre ord fungerer et potensiometer som en variabel spenningsdeler der spenningsdelingsforholdet er satt av viskerposisjon.
Denne applikasjonen av potensiometeret er et veldig nyttig middel for å oppnå en variabel spenning fra en fast spenning kilde, for eksempel et batteri. Hvis en krets du bygger krever en viss mengde spenning som er mindre enn verdien av et tilgjengelig batterispenning, kan du koble de ytre terminalene til et potensiometer over det batteriet og «ringe opp» hvilken spenning du trenger mellom potensiometeret. visker og en av de ytre terminalene for bruk i kretsen din:

Når det brukes på denne måten, gjør navnet potensiometer perfekt følelse: de måler (styrer) potensialet (spenningen) som påføres over dem ved å skape et variabelt spenningsdelingsforhold. Denne bruken av det tre-terminale potensiometeret som en variabel spenningsdeler er veldig populær i kretsdesign.
Prøver av små potensiometre
Her vises flere små potensiometre av den typen som vanligvis brukes i forbrukerelektronisk utstyr og av hobbyister og studenter i konstruksjon av kretser:

De mindre enhetene helt til venstre og veldig høyre er designet for å plugges inn i lodder s brødbrett eller loddes på et kretskort. Midtenhetene er designet for å monteres på et flatt panel med ledninger loddet til hver av de tre terminalene. Her er tre potensiometere til, mer spesialiserte enn settet som er vist:

Den store «Helipot» -enheten er et laboratoriepotensiometer designet for rask og enkel tilkobling til en krets. Enheten i nederste venstre hjørne av fotografiet er av samme type potensiometer, bare uten etui eller 10-trinns tellerhjul. Begge disse potensiometrene er presisjonsenheter, som bruker dreie motstandsstrimler for spiralskinne og viskermekanismer for å gjøre små justeringer. Enheten nederst til høyre er et panelmontert potensiometer, designet for grov service i industrielle applikasjoner.
ANMELDELSE:
- Seriekretsdeler, eller del, den totale forsyningsspenningen blant individuelle spenningsfall, proporsjonene er strengt avhengig av motstander: ERn = ETotal (Rn / RTotal)
- Et potensiometer er en variabel- motstandskomponent med tre tilkoblingspunkter, ofte brukt som justerbar spenningsdeler.
RELATERT WO RKSHEETS:
- Arbeidsark for spenningsdelerkretser